In diesem Kapitel finden Sie zwei Leserbeiträge zum Software-Experiment, die stellvertretend für zahlreiche weitere Zuschriften anläßlich dieser Serie stehen, und als Zugabe die CPC-Version eines Beitrags, der ursprünglich in der Zeitschrift PASCAL International veröffentlicht wurde.
Bereits im zweiten Kapitel wurden sich selbst organisierende Systeme und Zellautomaten behandelt. Eine besonders interessante und zudem grafisch sehr reizvolle Variante dieses Themas haben wir Herrn Brinkmann aus Ankum zu verdanken.
Das Programm Zellautomat (ZAUTOMAT.BAS) ist ein Hilfsmittel für die grafische Darstellung eindimensionaler Zellautomaten. Im Gegensatz zum Game of Life, das sich auf einer Fläche ausbreitet, entwickelt sich der eindimensionale Zellautomat entlang einer Linie. Das Schicksal einer Zelle in der folgenden Generation wird dabei vom Zustand der linken und rechten Nachbarzelle und der betrachteten Zelle bestimmt. Indem man Generation auf Generation untereinander anordnet, ist es möglich, die ganze Entwicklung in einem Bild sichtbar zu machen. Die Logik bzw. die Regeln des jeweiligen Zellautomaten können vom Benutzer frei definiert werden.
Theoretisch sind 410 (mehr als 1 Million) verschiedene Zuordnungen denkbar. Davon sind allerdings die meisten uninteressant. Solche Zellautomaten können nicht nur hübsche Grafiken erzeugen, sondern auch als Modell für physikalische Prozesse wie z.B. turbulente Strömungen dienen. Ebenso vermutet man, daß einige der eindimensionalen Zellautomaten genau wie das Game of Life universale Rechner sind.
Die Zellen (hier 320 pro Zeile) können die Werte 0, 1, 2, und 3 annehmen und werden auf dem Bildschirm durch einen Punkt in der entsprechenden PEN-Farbe dargestellt. Um die nächste Generation zu berechnen, sind jeweils drei nebeneinander liegende Werte zu addieren. Dem Ergebnis wird in einer Zuweisungstafel eine Zahl zugeordnet, die den Zustand der mittleren Zelle in der nächsten Generation bestimmt. Dazu ein Beispiel:
| Summe der drei Zellenwerte: | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| Neuer Wert der mittleren Zelle: | 0 | 3 | 1 | 0 | 2 | 0 | 2 | 3 | 1 | 3 |
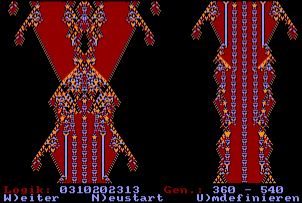
Das folgende Bild zeigt, wie sich diese Zuweisungstafel grafisch auswirkt. Das angegebene Beispiel ist der Zellautomat, der nach dem Start des Programms zu Verfügung steht. Da die obere Zeile der Tabelle immer gleich bleibt, wird durch die Angabe der unteren Zeile der Zellautomat vollständig definiert.

Und jetzt einige Hinweise zur Bedienung: Nach dem Start des Programms ZAUTOMAT.BAS erscheint am oberen Bildrand ein Pfeil, am unteren Bildrand die X-Position dieses Pfeils, und der Computer erwartet die Eingabe der Anfangspunkte. Wird die <COPY>-Taste gedrückt, so erscheint direkt über dem Pfeil in der obersten Bildschirmzeile ein Punkt in der Farbe von PEN 1. Durch mehrmaliges Drücken erhält er dann die Farbe 2, 3 oder wird gelöscht. Der Pfeil selbst wird durch die Cursortasten <links> bzw. <rechts> gesteuert. Nach der Eingabe der Anfangspunkte können Sie den Zellautomaten mit der <RETURN>-Taste starten. Der Aufbau des Bildes läßt sich jederzeit durch das Drücken einer beliebigen Taste unterbrechen, und Sie gelangen in ein kleines Menue. Hier stehen die folgenden drei Punkte zur Verfügung:
W)eiter: Die Ausgabe eines begonnenen Bildes wird fortgesetzt bzw. die Ausgabe der nächsten 10 Generationen begonnen.
N)eustart: Hier gelangen Sie wieder in den Eingabemodus für die Anfangspunkte.
U)mdefinieren: In diesem Unterpunkt können Sie ein neues Logikmuster definieren, indem Sie wie bereits erläutert die untere Zeile der Zuweisungstafel ohne Kommas und Zwischenzeichen eingeben. Die folgende Tabelle zeigt noch einige interessante logische Muster zum Ausprobieren. Mit der selbst zu definierenden Zuweisungstafel und den Anfangsbedingungen sind geradezu unerschöpfliche Experimentiermöglichkeiten gegeben
| Summe der drei Zellenwerte: | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| Neuer Wert der mittleren Zelle: |
0 | 2 | 3 | 0 | 1 | 0 | 3 | 2 | 3 | 1 |
| 0 | 2 | 3 | 0 | 2 | 1 | 3 | 2 | 3 | 1 | |
| 0 | 2 | 1 | 1 | 3 | 3 | 2 | 2 | 0 | 3 | |
| 0 | 2 | 1 | 1 | 0 | 3 | 2 | 0 | 1 | 3 | |
| 0 | 1 | 2 | 1 | 3 | 0 | 2 | 3 | 2 | 2 | |
| 0 | 1 | 2 | 1 | 3 | 1 | 0 | 0 | 0 | 0 |
Nicht so groß wie erhofft war leider die Resonanz auf die im Rahmen des Software-Experiments gegebene Anregung, Methoden und Programme zu erfinden, die mathematische Strukturen auf dem CPC nicht nur sichtbar, sondern auch hörbar machen. Das ist eigentlich verwunderlich, da schon die Grundlagen der Musiktheorie voller Mathematik sind. Herr Winkelmann aus Hannover zeigt in dem folgenden Beitrag, wie sich mit dem Computer auf mathematische Weise neue Wege der Klangerzeugung beschreiten lassen, für die konventionelle Musikinstrumente gar nicht oder nur eingeschränkt benutzbar sind:
Die gewohnte (europäische) Musik teilt eine Oktave in zwölf Schritte, die sogenannten Halbtonschritte auf. Daraus ergibt sich die Frage, ob man eine Oktave nicht auch in eine andere Anzahl von Schritten einteilen kann. Um diese Idee zu realisieren, muß man jedoch zunächst einmal wissen, mit welcher mathematischen Gesetzmäßigkeit sich die gewohnten Tonschritte berechnen lassen. Bei der Oktave ist das noch relativ einfach; sie entspricht der doppelten Frequenz, somit muß also die Tonperiode im Soundbefehl (zweiter Parameter) halbiert werden. Dazu ein kurzes Beispielprogramm:
100 INPUT "Grundperiode:",grund 110 oktave=grund/2 120 REM Grundperiode spielen 130 SOUND 7,grund,200,7 140 REM Oktave spielen 150 SOUND 7,oktave,200,7 160 REM Beide gleichzeitig 170 SOUND 1,grund,300,7 180 SOUND 2,oktave,300,7
Bei den Halbtonschritten ist die Berechnung auch nicht viel schwieriger, wenn man weiß, daß bei temperierter Stimmung zwischen den Frequenzen eine einfache mathematische Beziehung besteht:
| Grundton | a | 440 * 20/12 Hertz |
| kleine Sekunde | b | 440 * 21/12 Hertz |
| große Sekunde | h | 440 * 22/12 Hertz |
| kleine Terz | c | 440 * 23/12 Hertz |
...und so weiter. Der Zähler im Exponenten entspricht also der Anzahl der Halbtonschritte. Damit wäre das Problem gelöst, und man kann ein kurzes Programm schreiben, das die Halbtonschritte hörbar macht. Dabei ist jedoch zu beachten, daß zwischen den Tonperioden im SOUND-Befehl des CPC und den Tonfrequenzen ein reziprokes Verhältnis besteht. Man darf deshalb nicht mit den Potenzen von zwei multiplizieren, sondern muß durch diese dividieren, um eine aufsteigende Tonfolge zu erhalten. Diese Überlegungen führen zu folgendem Programm:
100 grundton = 284:REM Kammerton a 110 FOR halb = 0 TO 12 120 leiterton= grundton/2-(halb/12) 130 Sound 7,leiterton,100,7 140 NEXT halb
Um nun aber die Oktave in eine andere Anzahl Töne als die gewohnten zwölf zu unterteilen, ersetzt man die 12 in den Zeilen 110 und 120 einfach durch die gewünschte Anzahl. So kommt man zu dem folgenden Programm:
100 INPUT "Unterteilung:",anz.ton 110 grundton = 284 120 FOR schritt = 0 TO anz.ton 130 leiterton = grundton /2-(schritt/anz.ton) 140 SOUND 7,leiterton,100,7 150 NEXT schritt
Mit Hilfe dieser Anregung sollte es jedem möglich sein, sich eine Tabelle mit ungewöhnlichen Tonschritten zu berechnen und damit zu experimentieren. Besonders interessant ist die Einteilung der Oktave in 24 Schritte, weil man einerseits weiterhin die gewohnten Halbtöne zur Verfügung hat, andererseits aber auch dazwischenliegende Vierteltöne.
Neben der heute bei Instrumenten wie Klavier oder Gitarre üblichen temperierten Stimmung, die eine Oktave in zwölf gleiche Halbtonschritte unterteilt, gibt es bei einigen Instrumenten wie z.B. der Geige immer noch die sogenannte reine Stimmung, bei der die Frequenzen der Töne bestimmte ganzzahlige Verhältnisse ergeben. Diese Art der Stimmung hat zur Folge, daß ein Geiger den Ton Es anders greift als den Ton Dis, obwohl dies in der temperierten Stimmung die gleichen Töne sind. Die heute übliche temperierte Stimmung ist eigentlich nur eine gute und praktische Annäherung an die ursprüngliche reine Stimmung; sie hat es zum Beispiel erst möglich gemacht, ein Instrument wie das Klavier zu konstruieren, auf dem sich alle Tonarten gleichberechtigt benutzen lassen.
Jedoch bietet sich auch die reine Stimmung für Experimente an. Als Einstieg soll das Programm Frequenzverhältnisse (SOUND1.BAS) dienen, das die Verhältnisse zwischen den Frequenzen hörbar macht. Nach Eingabe einer Grundfrequenz und eines Verhältnisses wird die zweite Frequenz berechnet. Die beiden Töne werden zunächst nacheinander und darauffolgend im Zusammenklang gespielt.
Beim Experimentieren mit diesem kurzen Programm stellt man schnell fest, daß einfache Zahlenverhältnisse Konsonanzen (harmonisch zusammenklingende Töne) ergeben; je einfacher das Verhältnis, desto schöner der Klang. Und tatsächlich ergeben sich in reiner Stimmung für die gebräuchlichen Konsonanzen folgende Frequenzverhältnisse:
| Prime | 1:1 | Große Terz | 5:4 | |
| Oktave | 2:1 | Kleine Terz | 6:5 | |
| Quinte | 3:2 | Große Sexte | 5:3 | |
| Quarte | 4:3 | Kleine Sexte | 8:5 |
Der Grad der Konsonanz nimmt hier von oben nach unten ab. Im Mittelalter wurden nur solche Intervalle als konsonant empfunden, bei denen Zähler und Nenner des Verhältnisses zwischen 1 und 4 lagen, also die Prime, die Quarte, die Quinte und die Oktave. Inzwischen werden auch die anderen vier aufgeführten Intervalle als Konsonanzen wahrgenommen. Durch die häufige Verwendung von Septakkorden und ähnlichen Dissonanzen in der heutigen Musik wird das Konsonanzempfinden wahrscheinlich weiter abflachen und der Unterschied zwischen Konsonanz und Dissonanz in Zukunft immer mehr verwischt werden.
Auch hier lassen sich mit dem Computer prinzipiell neue Wege beschreiten. So könnte man zum Beispiel mit der Unterteilung der Oktave in 24 Töne einen Dreiklang aufbauen, der zwischen Dur und Moll liegt. Beim Dur-Dreiklang liegt auf einem Grundton eine große Terz und eine reine Quinte (z.B. C-E-G), beim Moll-Dreiklang hingegen liegt auf dem Grundton eine kleine Terz und eine reine Quinte (z.B. D-F-A). Wenn man nun einen Dreiklang aufbaut aus einem Grundton, einer reinen Quinte und dem Ton zwischen kleiner und großer Terz, so erhält man einen Akkord, der zwischen Dur und Moll liegt. Hörbar wird er durch das Programm SOUND2.BAS. Hier liegt sicherlich noch ein weites Feld für eigene Experimente!
Nach diesem Abstecher in die Welt der Klänge zurück zur Grafik: Der folgende Beitrag aus eigener Feder hätte hervorragend in die Serie Das Software-Experiment hineingepaßt, entstand aber leider zu spät. Er wurde anstattdessen in der Ausgabe 10/87 der Zeitschrift PASCAL International veröffentlicht und demonstriert, wie sich mit erstaunlich einfachen Mitteln verborgene Strukturen im Pascalschen Dreieck sichtbar machen lassen. Hier soll nun das Versäumte mit der entsprechenden Basic-Version (TRIANGLE.BAS) nachgeholt werden, womit wir wieder an das Thema des ersten Kapitels anknüpfen und sich der Kreis schließt.
Am Anfang war das Nichts: Ein unendliches Zahlenfeld aus lauter Nullen, vollkommen homogen, in jeder Hinsicht symmetrisch.
0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0
Doch hinter dieser monotonen Gleichförmigkeit verbarg sich ein Gesetz, das alle Zahlen zueinander in Beziehung setzte, ein unsichtbares Kraftfeld:
Jede Zahl ist gleich der Summe der links und rechts darüberliegenden Zahl,
und die Nullen gehorchten dem Gesetz auf absolut nichtssagende Weise, ohne ihm Ausdruck verleihen zu können. Doch genau wie unser physikalischer Raum seine Eigenschaften erst dann offenbart, wenn er Materie enthält, so zeigte das Zahlenfeld eines Tages seinen wahren Charakter, als sich unvermittelt eine kleine unscheinbare EINS dorthin verirrte, die grenzenlose Harmonie des sich selbst Entsprechenden mit einem Schlag durchbrach und quasi als Kondensationskeim eine Lawine von Zahlen auslöste, die sich unaufhaltsam bis in alle Unendlichkeit über die Ebene ergoß:
0 0 0 0 1 0 0 0 0
0 0 0 1 1 0 0 0
0 0 0 1 2 1 0 0 0
0 0 1 3 3 1 0 0
0 0 1 4 6 4 1 0 0
0 1 5 10 10 5 1 0
0 1 6 15 20 15 6 1 0
Auf einmal gab es größer und kleiner, gerade und ungerade, rechts und links, Richtung und Gegenrichtung... kurz gesagt, die Ebene hatte eine konkrete Struktur erhalten. Und diese Struktur ist dem Mathematiker wohlbekannt: Es handelt sich um das Pascalsche Zahlendreieck, das sich insbesondere nützlich erweist, um die Koeffizienten eines binomischen Ausdrucks der Form (a+b)n zu berechnen. Doch Zahlentabellen und Formeln können uns kaum vermitteln, was bei diesem mathematischen Schöpfungsakt wirklich entstanden ist, genausowenig, wie ein Notenblatt die Musik zum Erklingen bringt, die sie beschreibt. Obwohl die darstellende Mathematik eine recht alte Disziplin ist, hat sie eigentlich erst mit dem Computer ihr Musikinstrument erhalten, das mathematische Strukturen sicht- und hörbar macht und uns wie ein Mikroskop Einblicke in Welten verschafft, die uns sonst verschlossen blieben.

Trotzdem ist der programmtechnische Aufwand zur Erzeugung solcher Bilder oft erstaunlich gering. Das Programm TRIANGLE.BAS stellt im Prinzip nur fest, welche Zahlen des Pascalschen Dreiecks durch einen vorgegebenen Wert teilbar sind und markiert sie auf dem Bildschirm, durch einen Punkt - und das ist schon genug, um die in der Struktur verborgene Ordnung und Harmonie sichtbar zu machen. Um den Bildschirm gut auszunutzen, wird das Zahlenfeld um 45 Grad gekippt und auf einen quadratischen Ausschnitt begrenzt. Da die Zahlen des Dreiecks ziemlich schnell anwachsen und den Rechenbereich und die Genauigkeit der CPC-internen Zahlendarstellung überfordern, rechnet das Programm nur mit dem durch MOD ermittelten Divisionsrest weiter, wodurch sich das grafische Ergebnis jedoch nicht ändert.
Nach dem Programmstart brauchen Sie nur einen ganzzahligen Wert größer 1 einzugeben und <RETURN> zu drücken, worauf der CPC dann das dazugehörige Bild berechnet. Wenn es fertig ist, wartet der Rechner auf einen beliebigen Tastendruck, um danach einen neuen Teiler in Empfang zu nehmen. Wer mit dem Programm etwas experimentieren möchte, kann versuchen, dem Divisionsrest in der Variablen r2(spalte) verschiedene Farben zuzuordnen. Die Zeile 220 könnte dann beispielsweise so aussehen (MOD 4 begrenzt nur den Zahlenbereich auf gültige PEN-Nummern):
220 PLOT spalte*2+120,Zeile*2,r2(spalte) MOD 4
Der Algorithmus entstammt dem Buch Kunst! Computer? von KarlHeinz Koch (tewi-Verlag), das neben vielen philosophischen Bezügen und kritischen Anmerkungen zur Computerkunst noch zahlreiche weitere Experimente dieser Art enthält. Zwar sind die meisten Programm in Atari-Basic (800 XL) und für die Ausgabe auf einem Matrixdrucker geschrieben. Die ausführliche Dokumentation erleichtert es jedoch, die angewendeten Verfahren auf den CPC zu übertragen.