In der Januarausgabe 1987 der Zeitschrift PC International wurde den Lesern die Aufgabe gestellt, ein Programm zu entwickeln, das zwei beliebige Wörter durch eine Wortkette verbindet, wobei jeweils nur ein Buchstabe ausgetauscht werden darf. Als besonders harte Nuß hatten wir das Problem präsentiert, auf diese Weise GELD in BIER zu verwandeln und weiterhin die Frage aufgeworfen, ob es überhaupt möglich ist, mit einem Mikrocomputer wie dem CPC Rätsel dieser Art generell zu lösen. Die Leserschaft ließ jedoch nicht lange auf eine Antwort warten: Bereits kurz nach Erscheinen von Heft 1/87 trafen die ersten Programm zu diesem Thema in der Redaktion ein, und nach einigen Tests und Experimenten mit dem Material blieb nur noch die Feststellung: Das Problem ist in der Tat gelöst!
Man sollte wirklich nicht das in der Mikrocomputerszene vorhandene kreative Potential unterschätzen: Hier werden unbehelligt von ökonomischen Zwängen oder wissenschaftlichen Zielsetzungen auf spielerische Weise Problem gelöst, die Profis mitunter nur ein müdes "Dazu brauche ich einen größeren Rechner" entlocken. Herr Raab aus Nimtofte, Dänemark, der sich ebenfalls mit dem Wortketten-Problem beschäftigt hat, schrieb dazu: "Die tägliche Arbeit mit dem Computer läßt einem kaum Zeit für dergleichen, und die meisten Computersysteme heutzutage sind so komplex, daß man sich keine Experimente erlauben kann. Da ist der Computer zu Hause viel besser. Er ist zwar etwas langsam, aber dafür kann ich damit machen, was ich will, wenn das Gerät nicht gerade von meinen Söhnen beschlagnahmt ist.
Und wer unvorsichtigerweise den Ehrgeiz der MicrocomputerFreaks herausfordert, muß wissen was er tut: Gerade die Firma Commodore, die mit ihrem C 64 einiges zu dieser Entwicklung beigetragen hat, gehörte vor einiger Zeit zu den Leidtragenden, als die Wundermaschine Amiga der Öffentlichkeit präsentiert wurde. Wer kennt nicht den berühmten "Bouncing Ball", der als bildschirmfüllendes Makro-Sprite neue Maßstäbe bei animierter Grafik setzte? Natürlich dauerte es nicht lange, bis der lästige Konkurrent Atari auf seinem ST mit einer getreuen Kopie der karierten Superkugel aufwarten konnte. Gut, beeilte man sich bei Commodore mitzuteilen, man möge aber bitte beachten, daß der Atari damit bereits zu 90% ausgelastet sei, während der Amiga dank seiner Spezialchips ohne weiteres noch gleichzeitig ein Präludium von Bach und eine Partie Schach spielen könne.
Das Argument hatte etwas für sich. Als jedoch wiederum nur kurze Zeit später auf allen möglichen Mikros bis hin zum Sinclair Spectrum der hüpfende Ball auftauchte, zog man es bei Commodore vor, der weiteren Entwicklung mit weiser Zurückhaltung zu begegnen. Auch für den CPC existiert übrigens ein verblüffendes "Bouncing Ball"-Programm, bei dem gleich eine ganze Legion von Bällen auf dem Bildschirm vor einem bewegten Hintergrund (!) herumhüpft. Dieses Grafik-Demo, das in PC International 7/88 veröffentlicht wurde, muß man einfach sehen, um es zu glauben!
Das alles schmälert zwar nicht die Leistungsfähigkeit des Amiga als Grafikmaschine, zeigt aber, daß die 8-Bit-Zwerge immer noch nicht ausgereizt sind. Gerade die hardwaremäßigen Beschränkungen scheinen die Programmierer zu immer neuen Taten anzuregen, und von daher hätte man es sich eigentlich denken können: Die im 7. Kapitel angedeuteten Zweifel, ob eine Lösung des Wortkettenproblem auf einem CPC überhaupt möglich ist, waren für die PC International-Leser eine echte Herausforderung.
An dieser Stelle soll zunächst die Lösung des GELD/BIER-Rätsels verraten werden:
GELD - HELD - HERD - HERR - HEER - TEER - TIER - BIER
So geht's - und wenn man das Wort HIER zuläßt, kommt man sogar noch mit einem Schritt weniger aus. Um solch ein Rätsel zu lösen braucht der Computer genau wie ein Mensch einen gewissen Wortschatz. Welchen Einfluß der Umfang und die Zusammensetzung der Wortliste hat, beschreibt Herr Mühlenweg aus Krefeld: "Ob eine Transformation einfach (z.B. GERD-WOLF) oder schwierig ist, hängt nur vom Vokabular des Rechners ab. Fehlt beispielsweise das Wort GOLD, so wird aus dem einfachen ein schwieriges oder sogar unlösbares Problem".
Ein sehr großer Wortschatz ist allerdings noch keine Garantie für überragende Fähigkeiten bei der Suche nach Wortketten. Schließlich muß der Rechner ja geeignete Wörter herausfiltern. Gerade das GELD /BIER-Problem leistet dabei einigen Widerstand. Nach welchem System kann man zum Beispiel erkennen, daß die Umwandlung in HELD einen geeigneten Ansatz darstellt? Herr Raab stellt die grundlegenden Schwierigkeiten auf sehr anschauliche Weise dar: "Zur Lösung des Problems braucht man ein Maß dafür, wie weit man zu jedem Zeitpunkt von dem gesetzten Ziel, also dem Wort BIER, entfernt ist. Die Anzahl der unterschiedlichen Buchstaben im Zielwort und einem Vergleichswort ist ein natürliches Maß für diesen Abstand. Stellt man sich das Zielwort als Berggipfel vor, so kann man die Differenz als Luftlinienabstand ansehen. Leider haben wir kein Maß für den Weg, den wir zurücklegen müssen, wenn wir nicht fliegen können, sondern auf einen Pfad angewiesen sind, d.h. auf benachbarte Wörter".
Der Computer als Pfadfinder in unwegsamen Gelände - es wird klar, daß es wohl kaum ohne einen effektiven Suchalgorithmus geht, der den Pfad durch Versuch und Irrtum ermittelt. Das erste Programm, das auf diese Weise eine Lösung anstrebt, traf bereits Anfang Januar ein und stammt von Herrn Klaas Wedemeyer aus Hamburg. Es benutzt ein sich selbst aufrufendes (rekursives) Unterprogramm, das zu dem Startwort ein benachbartes Wort (ein Buchstabe verschieden) aus der Liste sucht, zu diesem Wort wieder ein benachbartes Wort, und so weiter. Gerät das Programm dabei in eine Sackgasse, so kehrt es automatisch zum vorherigen Schritt zurück und probiert eine andere Fortsetzung. Endlosschleifen werden verhindert, indem jeder Kandidat daraufhin überprüft wird, ob er schon in der Wortkette vorkommt.
KI-Experte Martin Schlöter von PASCAL International hatte auch sofort den passenden Fachausdruck parat, als ich ihm das Programm zeigte. "Diese Methode, bei der der Computer in seiner eigenen Spur zurückwandert, um eine andere Abzweigung zu finden, heißt Backtracking und ist in der Sprache PROLOG gleich eingebaut", erläuterte er und murmelte dann noch etwas, daß sich wie "sowas macht man auch nicht in BASIC" anhörte. Bevor er sich wieder in die höheren Regionen der Programmierkunst zurückzog, gelang es mir jedoch, ein kleines LOGO-Programm abzustauben, daß die Rekursion sehr anschaulich grafisch darstellt:
to Baum :Länge :Winkel :Tiefe if :Tiefe 0 then [stop] fd :Länge rt :Winkel / 2 Baum :Länge * 0.9 :Winkel :Tiefe - 1 lt :Winkel Baum :Länge * 0.9 :Winkel :Tiefe - 1 rt :Winkel / 2 bk :Länge end
Das LOGO-Programm malt also einen Baum und nutzt dabei die Tatsache aus, daß jeder Ast mit seinen Verzweigungen wieder als Baum betrachtet werden kann; die Routine braucht sich also nur selbst aufzurufen. Starten Sie, falls vorhanden, Ihren LOGO-Interpreter, tippen Sie das Listing ab und geben Sie dann z.B. ein:
Baum 50 60 4
Der erste Parameter bestimmt die Länge der Äste, der zweite den Öffnungswinkel bei einer Verzweigung und der dritte die Rekursionstiefe. Betrachtet man den Weg der Schildkröte auf dem Bildschirm so kann man sich gut vorstellen, wie der Suchvorgang in der Wortliste abläuft: Hat das grafisch talentierte Reptil einen Endpunkt im Baum erreicht, so klettert es wieder abwärts, um an einer anderen Stelle weiterzumalen, an der noch eine Verzweigung fehlt.
Das Prinzip sieht auf den ersten Blick vielversprechend aus; die ersten Versuche mit einer umfangreichen Wortliste verliefen jedoch enttäuschend: Da ja alle denkbaren Folgen ohne Einschränkung untersucht werden, verirrt sich der Rechner ziemlich schnell in endlosen Wortketten. Zwar garantiert das Verfahren, daß alle existierenden Lösungen gefunden werden (egal wie lang), braucht dazu jedoch sehr viel Zeit. Außerdem interessiert eine Lösung in 20 Schritten kaum, wenn es auch eine in 6 Schritten gibt. Was also tun? Doch die Frage war bald beantwortet: Nur kurze Zeit später traf das Listing von Herrn Mühlenweg ein, mitsamt einigen weiteren Ideen.
In seinem Programm wird der Benutzer zu Beginn gefragt, wieviele Schritte die Kette maximal enthalten soll, wodurch zwar eine längere Lösung hinter dem Suchhorizont verschwindet, aber dafür die Rechenzeit kontrollierbar wird. Zusätzlich sieht der Autor noch eine weitere Möglichkeit, die Rechenzeit zu verkürzen: "Wenn keine Aussicht mehr besteht, daß in den verbleibenden Suchbaumetagen (bis zum vorgegebenen Suchhorizont) noch alle ungleichen Buchstaben ausgetauscht werden können, kommt das betreffende Wort nicht mehr in Frage. Der Suchaufwand wird hierdurch sicherlich reduziert, ohne daß sich das Ergebnis ändert"
Befinden sich z.B. zwei Schritte vor dem Ende der Kette noch drei falsche Buchstaben in einem Wort, wird es überhaupt nicht mehr in Betracht gezogen. Diese zielgerichtete Suche vermeidet in der Tat eine Menge Irrwege. Störend macht sich nur bemerkbar, daß das Programm immer wieder auf Umwege hereinfällt, wie etwa
HASE - NASE - VASE
Von HASE nach VASE hätte auch ein Schritt gereicht, wie man sofort sieht. Doch auch hier gibt es Abhilfe: Es muß nur abgefragt werden, ob sich ein Wort vom vorvorigen Wort der Kette in nur einem Buchstaben unterscheidet. Ist das der Fall, so liegt offensichtlich ein Umweg vor, und das Wort wird verworfen. Zwar vermeidet diese Abfrage nicht alle Umwege (sie können sich ja über mehr als drei Schritte erstrecken), eliminiert aber den häufigsten Fall wirkungsvoll. Im Prinzip könnte man diesen Test auf weitere Wörter der Kette ausdehnen, es fragt sich nur, ob dadurch auf Dauer nicht mehr Zeit verbraucht als eingespart wird.
So weit, so gut - faßt man diese Ideen zusammen, so erhält man bereits ein recht brauchbares Programm. Das BASIC-Programm WKETTE1.BAS zeigt, wie die verschiedenen Elemente realisiert werden. Als Arbeitsgrundlage dient eine Liste vierbuchstabiger Wörter (LISTE4.DAT), die bereits im letzten Kapitel von WORDMASTER benutzt wurde und vom Wortketten-Programm in den Zeilen 190 - 250 in das Array wort$ geladen wird, bevor der Benutzer das Rätsel eingibt.
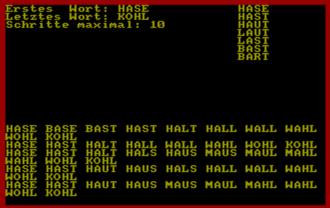
Nach dem Start mit RUN "WKETTE1" erwartet das Programm zunächst drei Eingaben von Ihnen, die jeweils mit <RETURN> bestätigt werden: Das vierbuchstabige Startwort, das Endwort, und die Anzahl Schritte, die maximal zur Bildung der Wortkette erlaubt sind.
Die Hauptarbeit leistet das rekursive Unterprogramm ab Zeile 450. Die aktuelle Suchebene ist in der Variablen schritt vermerkt; sie wird bei jedem Aufruf um 1 erhöht. Weiterhin existiert für jede Ebene ein Zeiger, der das gerade untersuchte Wort in der Liste (d.h. im Array wort$) markiert. Bevor nun ein Kandidat als nächstes Glied der Kette akzeptiert wird, muß er einige strenge Prüfungen über sich ergehen lassen. Fällt er durch, so springt das Programm sofort nach Zeile 890, wo der Zeiger auf das nächste Wort gerichtet wird. Ist das Ende der Wortliste erreicht, so wird die Variable schritt um 1 vermindert, und das Programm kehrt auf die vorherige Ebene zurück.
Erfüllt der Kandidat jedoch alle Kriterien, so wird er in Zeile 840 in das Array kette$ eingetragen. Beträgt die Differenz zum Zielwort (zdif) an dieser Stelle nur noch 1, so liegt eine Lösung vor, die mit GOSUB 960 angezeigt wird; andernfalls ruft die Routine sich mit GOSUB 450 selbst auf, um die Kandidaten für den nächsten Schritt zu untersuchen. Auf dem Bildschirm kann man dabei sehr schön beobachten, wie das Programm die Wortketten auf- und notfalls auch wieder abbaut, falls sie nicht zum gewünschten Ziel führen.
Nein, das ist unser Programm mit Sicherheit nicht. Um es gut lesbar zu gestalten, wurde bewußt darauf verzichtet, mit allen Tricks und Kniffen eine maximale Geschwindigkeit zu erreichen. Ambitionierte Bastler können hier mit Sicherheit noch einiges herausholen. Aber abgesehen von programmtechnischen Fragen: Ist dieser Algorithmus wirklich die einzige Methode, um das Wortkettenproblem zu lösen? Weitere Leserzuschriften beweisen, daß es durchaus noch Alternativen gibt. Sie beruhen auf der Idee, die Wortliste im Speicher gleich von vornherein so zu strukturieren, daß eine besonders effektive Suche möglich wird.
Herr Maleschka aus Hagen schickte uns z.B. ein Pascal-Programm mit folgender Idee: "Die Daten werden im Speicher in sogenannten Inseln abgelegt. Das Besondere an den Wörtern einer Insel ist, daß man von jedem Wort einer Insel zu jedem anderen Wort der Insel mit Sicherheit einen Weg findet." Gleich bei der Eingabe eines neuen Wortes wird untersucht, ob es in den bereits bestehenden Inseln einen Nachbarn gibt. Ist das der Fall, so wird es dort einsortiert. Finden sich auf mehreren Inseln Nachbarn, so bildet das Wort quasi eine Brücke zwischen den Wortgruppen, und sie werden zusammengefaßt. Der Vorteil liegt auf der Hand: Das Programm kann sehr schnell feststellen, ob es überhaupt eine Lösung gibt (Start- und Zielwort müssen sich ja gemeinsam auf einer Insel befinden!) und kann bei der Suche die überseeischen Gebiete vollkommen außer acht lassen.
Bei der Strukturierung von Daten tut sich BASIC allerdings recht schwer. Abgesehen von den unflexiblen Arrays werden keine Hilfsmittel geboten, im Gegensatz zu Pascal: Mit Records, Pointern und verketteten Listen stellen komplexe Datenstrukturen kein Problem dar. Man kann allerdings auch die andere Richtung wählen und in die Tiefen der Assemblerprogrammierung herabsteigen, wo sich Daten ebenfalls sehr flexibel verwalten lassen - zwar nicht so komfortabel und ohne Sicherheitsgurte, aber dafür sehr flott. Herr Gerald Steffens aus Harsewinkel hat diesen Weg eingeschlagen und ein Programm eingesandt, daß in der Tat beeindruckende Leistungen zeigt. Es ordnet die Wortliste im Speicher in Form eines Graphen an: Zu jedem Wort existiert eine Gruppe von Zeigern, die die Speicheradressen der benachbarten Wörter angeben. Schreibt man alle Wörter auf ein großes Blatt Papier und verbindet die benachbarten Wörter durch Linien, so hat man die Struktur bildlich vor Augen.
Den Graphen muß der Rechner nur einmal zu Beginn aufbauen (außer es kommen neue Wörter hinzu), und danach geht die Post ab: Da das Programm die benachbarten Wörter nicht mehr mühsam suchen muß, sondern gleich einen entsprechenden Hinweis im Speicher findet, kann es sich in Windeseile durch den Graphen hindurchhangeln. Weiterhin hilft ein fundierter theoretischer Hintergrund bei der Programmierung: "Die reine mathematische Idee, die übrigbleibt, wenn man das Problem analysiert, findet sich in der Graphentheorie und Kombinatorik wieder", schreibt Herr Steffens und führt in diesem Zusammenhang den Algorithmus von Dijkstra an, den er auch in seinem Programm als Grundlage benutzt hat.
Leider reicht der Platz nicht, um diese Methode ausführlich zu diskutieren, deshalb nur soviel: Es handelt sich im Prinzip um einen Labyrinth-Algorithmus, der mit nachtwandlerischer Sicherheit den kürzesten Weg im Graphen ermittelt, und zwar nicht nur zu einem vorgegebenen Zielwort, sondern gleich zu allen erreichbaren Punkten. Es ist schon beeindruckend, wie das Programm nach Eingabe des Startwortes eine Liste aller überhaupt nur möglichen Zielwörter ausspuckt, mitsamt der minimalen Schrittzahl, in der sie erreicht werden können. Nach Eingabe eines der Wörter wird dann prompt die dazugehörige Kette geliefert. Natürlich hat man auf diese Weise auch gleich eine große Anzahl potentieller Aufgaben zur Auswahl - also das ideale Programm für eine Rätselzeitschrift!
Das Programm besteht aus zwei Teilen. Zuerst wird der Lader für den Maschinencode mit RUN "WKETTE2" gestartet, worauf dieser dann automatisch das Hauptprogramm KETTEV2 nachlädt. Hier noch ein paar Erläuterungen zu den Punkten des Hauptmenues:
Laden: Es kann wahlweise eine Wortliste im Binär- oder im ASCIIFormat geladen werden. LISTE4.DAT auf Ihrer Diskette/Kassette ist eine ASCII-Datei.
Speichern: Die Wortliste wird nach Angabe einer Dateinummer binär abgespeichert.
Ausgabe: Die Liste wird auf dem Bildschirm ausgegeben.
Wort einfügen: Ein neues Wort kann eingegeben werden.
Korrektur: Ein falsches Wort wird gegen das richtige ausgetauscht.
Einstieg ins Suchprogramm: Dient zur Eingabe des Start- und Zielwortes.
Zurück ins Hauptmenue kommt man jederzeit durch Drücken von <ENTER> ohne eine vorherige Eingabe.
Damit liegt nun ein nahezu perfektes Wortketten-Programm vor, und es bleibt eigentlich nur noch, allen Lesern zu danken, die - genannt oder ungenannt - in ihren Beiträgen das Problem von allen Seiten beleuchtet, analysiert und schließlich gelöst haben. Durch ihre tatkräftige Mithilfe ist dieses Kapitel des Software-Experiments erst möglich geworden.