Hier als Einstimmung zunächst ein Zitat aus der Frankfurter Rundschau vom 3.11.1986:
"Während das Verhältnis des Vatikans zur Naturwissenschaft geklärt zu sein scheint - immerhin ist Galileo Galilei von Johannes Paul II. rehabilitiert worden, 350 Jahre nach dem Prozeß - ist im Verhältnis zu den Humanwissenschaften vielfach noch eine galileische Situation gegeben. Davon zeugt die jüngste Stellungnahme des Vatikans zur Homosexualität bei Männern und Frauen. 'Einzig in der Ehe kann der Gebrauch der Sexualkraft moralisch gut sein. Deshalb handelt eine Person, die sich homosexuell verhält, unmoralisch', lauten die beiden Kernsätze dieses Dokuments."
Die Entwicklung der modernen naturwissenschaftlichen Denkweise begann im 17. Jahrhundert, und als ihr geistiger Vater wird im allgemeinen Galileo Galilei angesehen. Wie man weiß, provozierte er damals mit seiner Behauptung, die Sonne und nicht etwa die Erde wäre der Mittelpunkt unseres Planetensystems, einigen Ärger. Die Vertreter der herrschenden Lehrmeinung verfügten jedenfalls über ausreichende Druckmittel, um ihn zum Widerruf zu veranlassen. Galileis berühmter Ausspruch auf dem Totenbett '...und sie bewegt sich doch' ist vielleicht nachträglich erfunden worden, steht aber symbolisch für die Tatsache, daß die zu seiner Zeit revolutionären Erkenntnisse trotz alledem nicht mehr aufzuhalten waren.
Die Legende berichtet, daß Galilei seine Widersacher aufforderte, durch das von ihm entwickelte Fernrohr zu schauen, um sich mit eigenen Augen von den Gesetzmäßigkeiten der Planetenbewegung zu überzeugen. Doch die Pharisäer und Schriftgelehrten lehnten ab: 'Warum sollen wir durch dein Rohr blicken, wo wir doch genau wissen, daß nicht sein kann, was du sagst...' Als Kinder des Weltraum-Zeitalters blicken wir heute verständnislos auf diese Mischung von Dummheit und Arroganz und fragen uns, wie so etwas möglich sein konnte - doch halt! Sind Sie, lieber Leser, bereit, für einen Moment eine selbstkritische Haltung einzunehmen? Dann denken Sie einmal über die folgenden Fragen nach: Woher wissen Sie eigentlich, daß sich die Erde um die Sonne dreht? Haben Sie es in der Schule gelernt, in einem Buch gelesen oder im Fernsehen gehört? Mal ganz ehrlich: Hätte man Ihnen auf diese Weise nicht auch die umgekehrte Meinung eintrichtern und Sie zu einem überzeugten Vertreter eines geozentrischen Weltbildes erziehen können, ohne daß Sie es jemals in Frage gestellt hätten?
Man muß sich in diesem Zusammenhang vor Augen halten, daß es zu Galileis Zeiten gang und gäbe war, alle wissenschaftlichen Erkenntnisse aus der Bibel oder den Schriften des klassischen Altertums abzuleiten. Galileis Faux Pas bestand weniger darin, den herrschenden Lehrmeinungen zu widersprechen; von Bedeutung war vielmehr, daß er die damals gültige wissenschaftliche Methodik von Grund auf ablehnte. Als Gegenpol zur Deduktion, der Anwendung vorgegebener Gesetzmäßigkeiten auf Einzelfälle (Naturphänomene), führte er das wissenschaftliche Experiment als Frage an die Natur ein, ob denn die in den Theorien enthaltenen Behauptungen überhaupt stimmen. Die Theologen seines Zeitalters sahen darin einen Versuch, die Theologie den Naturwissenschaften unterzuordnen und schickten Galilei die Inquisition auf den Hals, da sie verständlicherweise keine Lust hatten, ihre dominierende Position aufzugeben.
Die wissenschaftliche Methode im Sinne Galileis beinhaltet also eine ausgesprochen kritische Denkweise, die eine hohe geistige Beweglichkeit erfordert. Für sie gibt es keine gottgegebenen Gesetze, die als heilige Kühe im Marmortempel der Wissenschaft vor sich hin muhen. Jede Behauptung (ob aus der Bibel oder dem Fernsehen) stellt nur einen Anlaß dar, weitere Fragen zu stellen, die natürlich dazu führen können, daß der ursprüngliche Denkansatz total über den Haufen geworfen wird. Um diesen Vorgang noch einmal zusammenzufassen: Aus der Beobachtung einzelner Naturphänomene wird auf bestimmte Gesetzmäßigkeiten geschlossen (Induktion). Aus diesen Gesetzen läßt sich wiederum ableiten, wie sich die Natur in anderen Fällen verhalten wird (Deduktion). Experimentell wird geklärt, ob diese Voraussagen mit der Realität übereinstimmen. Ist das nicht der Fall, so muß die Theorie entsprechend modifiziert und als Ausgangspunkt für weitere Versuche benutzt werden. Aus diesem ständigen Wechselspiel von Induktion und Deduktion ensteht wissenschaftliche Erkenntnis, Theorie und Praxis arbeiten gleichberechtigt Hand in Hand.
Galilei gewann seine Erkenntnisse durch eine ständige Auseinandersetzung mit der Realität; er lehnte es ab, die Realität mit Gewalt so zu interpretieren, daß sie zu einem vorprogrammierten Wissen kompatibel wurde. Seine Methode stellt praktisch eine systematisierte Form des Lernens dar, und hier wird der KI-Programmierer hellhörig: Methode? System? Wo diese Begriffe auftauchen, ist häufig ein Algorithmus nichr mehr fern, ein in Einzelschritte auflösbares Verfahren, das auch von einer Maschine ausgeführt werden kann.
Und damit sind wir wieder bei der Frage angelangt, die uns bereits im letzten Kapitel beschäftigt hat: Wie kann ein Computer zu einem selbständigen Lernprozeß angeleitet werden? Immerhin hatten wir mit dem Minischach-Programm Teilerfolge vorzuweisen, die aber insgesamt nicht besonders befriedigten. Die Lernerfolge wurden praktisch nur durch eine gut organisierte Datenspeicherung erreicht, und das im Schneckentempo, da unser Programm aus seinen Erfahrungen keine allgemeingültigen Gesetzmäßigkeitenableiten konnte.
Bevor wir uns jedoch dem Problem zuwenden, einem Computer zumindest einen Schimmer echter Erkenntnisfähigkeit zu vermitteln, soll der Begriff 'Lernen' an dieser Stelle genauer betrachtet werden. In gewisser Weise kann ja schon die Programmierung eines Computers, also das Abspeichern einer Folge von Anweisungen, als Lernvorgang aufgefaßt werden. Doch diese Art des Lernens, die praktisch nur eine ausgeprägte Merkfähigkeit verlangt, ist für die künstliche Intelligenz nicht besonders interessant. Gefragt sind vielmehr Systeme, die aufgrund ihrer Erfahrungen von sich aus ihr Verhalten ändern, und das erfordert nicht nur ausreichend Speicherplatz, sondern auch eine hochentwickelte Auffassungsgabe, um die Folgen verschiedener Entscheidungen wahrzunehmen und zu verarbeiten.
Auch beim Menschen wird dieser Unterschied deutlich. Mit Sicherheit erfordert es mehr Intelligenz, eine Sprache zu lernen, als Vokabeln zu lernen: Im ersten Fall müssen komplexe Sinnzusammenhänge erfaßt werden, im zweiten Fall reicht ein gutes Gedächtnis. Es ist immer wieder faszinierend , mitzuerleben, mit welcher naturgegebenen Intelligenz sich ein kleines Kind die Sprache aneignet; erschreckend ist andererseits die Erkenntnis, daß sich Menschen in vieler Hinsicht wie Computer programmieren lassen.
Ein gutes Beispiel dafür bietet die Werbung, die durch vielfache Wiederholung und unterschwellige Beeinflussung unser Konsumverhalten steuern soll. Daß diese Art der Programmierung offenbar gut funktioniert, läßt sich allein daraus ablesen, daß die Wirtschaft Jahr für Jahr unverdrossen Milliarden investiert, um z.B. brave Hausfrauen davon zu überzeugen, daß sie ohne RENOL ein schlechtes Gewissen ihrer Familie gegenüber haben müssen.
Erinnern wir uns noch einmal an die unbequemen Fragen zu Beginn dieses Kapitels. Mit Sicherheit haben Sie bereits vieles in Ihrem Leben gelernt. Doch wie sieht es aus: Beruht das Gelernte auf Erkenntnissen, die durch Erfahrung und gezielte Fragen gewonnen wurden, oder auf einer durch Erziehung oder Medien vermittelten Programmierung? Wie auch immer das Ergebnis Ihrer Untersuchung ausfallen mag - diese Gegenüberstellung vermittelt ein Bild davon, worauf es bei einer 'künstlich intelligenten' Lernfähigkeit ankommt.
Nach wie vor ist die Realität mit allen ihren Aspekten zu komplex, um als Objektraum für die Programmierung künstlicher Intelligenz in Frage zu kommen. Alle Versuche beziehen sich deshalb auf einen genau definierten (und meist sehr kleinen) Ausschnitt der Realität oder auf ein stark vereinfachtes Modell realer Vorgänge. Wie bereits in den letzten Kapiteln deutlich wurde, eignen sich Spiele zu diesem Zweck ganz ausgezeichnet. Sie beschränken sich einerseits auf eine überschaubare Menge von Objekten (Spielfiguren) und Operationen (mögliche Spielzüge), enthalten aber auf der anderen Seite eine ausreichende Anzahl Unsicherheitsfaktoren (Züge des Gegners), auf die das Programm mit einer gewissen Selbständigkeit reagieren muß.
Auch die Anwendung wissenschaftlicher Methoden läßt sich sehr schön anhand eines Spiels demonstrieren, das vor einigen Jahren unter dem Titel 'Superhirn' oder 'Mastermind' in den Handel kam und sehr populär wurde. Im Prinzip geht es darum, einen geheimen Code zu knacken, der aus einer verdeckten Reihe farbiger Steckknöpfe besteht. Für jeden Code, den man ausprobiert, erhält man vom Gegenspieler eine Trefferquote, die über die Anzahl der richtigen Farben und richtigen Positionen Auskunft gibt. Durch logische Schlußfolgerungen und eine effektive Versuchsanordnung soll man dem Code möglichst schnell auf die Schliche kommen.
Wir werden uns in dieser Folge mit einer besonders reizvollen Variante dieser Spielidee beschäftigen, bei der mit dem gleichen Verfahren ein geheimes Wort gesucht wird - also das ideale Spiel für Hacker! Als Code oder Versuche kommen natürlich nur im Sprachgebrauch übliche Wörter in Frage, und man muß sich vor Spielbeginn auf eine bestimmte Wortlänge einigen. Hier gleich ein Beispiel: Gesucht ist das Wort HAUS; das Experiment DACH erhält dann als Trefferquote zwei richtige Buchstaben (A und H) und eine richtige Position (A steht an der richtigen Stelle). Im Folgenden weren wir die Ergebnisse kurzerhand so notieren,
DACH # +
mit zwei Markierungen für zwei richtige Buchstaben, wobei das Doppelkreuz für die richtige Position steht. Zu beachten ist, daß doppelt vorkommende Buchstaben nur dann zwei Treffer ergeben, wem sie auch im Geheimwort doppelt vorhanden sind. Der geheime Code HEXE kann z.B. folgende Versuchsergebnisse erzeugen:
HUHN # ESEL + +
Um sich dem geheimen Wort zu nähern, ist eine Auswertung der Trefferquoten unumgänglich, wobei man meist eine Reihe von Fällen durch logische Schlüsse ausklammern kann. Teilweise ist das sehr einfach: Wenn ein Wort keinen einzigen Treffer erhält, so kommen die Buchstaben in dem geheimen Code nicht vor. Etwas schwieriger wird es jedoch, wenn die ersten beiden Versuche das folgende Ergebnis bringen:
EHRE # WORT +
Hieraus geht eindeutig hervor, daß das geheime Wort kein R enthält - können Sie herausfinden, warum? Noch wesentlich komplizierter gestalten sich Schlußfolgerungen, die aus der gemeinsamen Betrachtung von drei oder mehr Versuchen entstehen, und oft ist man sogar auf Vermutungen angewiesen. Schauen Sie sich die folgenden Ergebnisse an:
BERG # # WERT # #
Es drängt sich der Verdacht auf, daß die Kombination ER in der Mitte für die beiden richtigen Positionen veranrwortlich ist; wie sollte es anders sein? Also hauen wir mit dem dritten Versuch in die gleiche Kerbe,
HERZ #
und erhalten nur eine richtige Position! Hier kann man ansatzweise nachempfinden, wie einem Wissenschaftler zumute ist, wenn durch das Ergebnis eines Experiments eine schon sicher geglaubte Theorie den Bach runter geht. Das geheime Wort in diesem Fall war übrigens BART...
Um sich ein vollständiges Bild von dem Charakter dieses Spiels zu verschaffen, suchen Sie sich am besten einen Partner und spielen ein paar Fälle durch. Dabei wird schnell klar, daß ein blindes Herumprobieren überhaupt nichts bringt. Eine gute Methode besteht jedoch darin, aufgrund der vorherigen Versuchsergebnisse eine Theorie über die Zusammensetzung des geheimen Wortes aufzustellen, wobei man mitunter bewußt in Kauf nimmt, daß sie auch falsch sein könnte. Der nächste Versuch wird dann wie in unserem letzten Beispiel dieser Arbeitshypothese entsprechend
formuliert; die Trefferquote gibt Auskunft darüber, ob die Annahmen berechtigt waren. Mit dieser naturwissenschaftlichen Strategie hat man eine klare Linie vor Augen, die relativ sicher zum Ziel führt. Alles, was uns jetzt noch fehlt, ist ein intelligentes Programm, das den geheimen Code ebenfalls knacken kann.
Zunächst taucht jedoch die Frage auf, ob wir uns nicht ein bißchen viel vorgenommen haben. Offensichtlich muß das Programm ja hochkomplizierte logische Schlüsse bewältigen können, Annahmen aufstellen und wieder verwerfen... brauchen wir hier nicht mindestens einen Großrechner und spezialisierte Programmiersprachen wie LISP oder PROLOG? Doch weit gefehlt - WORDMASTER demonstriert eindrucksvoll, daß auch ein Microcomputer in reinem BASIC dieses Problem lösen kann!

Nach dem Programmstart mit RUN "WMASTER" erwartet Sie das Hauptmenue, das unter anderem den Punkt Spielen anbietet. Wer hier sofort zugreift, wird jedoch eine Enttäuschung erleben: WORDMASTER verlangt zunächst eine Wortliste; ohne einen gewissen Grundwortschatz ist das Programm nicht aktionsfähig. Auf der Programmdiskette bzw. -kassette stehen Ihnen zwei fertige Wortlisten zur Verfügung (LISTE4.DAT, LISTE5.DAT), die Sie mit dem Menuepunkt <3> laden können. Eine enthält vier- und die andere fünfbuchstabige Wörter. Aufgenommen wurden nur im deutschen Sprachgebrauch übliche Hauptwörter ohne Umlaute und ß, weiterhin keine Eigennamen oder geographische Namen. Diese Einschränkungen haben sich in der Praxis als sinnvoll erwiesen; wie Sie sehen werden, ist das Spiel auch damit schon schwierig genug!
Der Menuepunkt <2> dient dazu, eine Wortliste einzugeben, zu verändern oder anzuzeigen; auf dem Bildschirm erhalten Sie alle notwendigen Hinweise. Zu beachten ist, daß bei der Eingabe einer neuen Liste das erste Wort die Länge aller weiteren Wörter bestimmt, abweichende Eingaben werden im Folgenden zurückgewiesen. WORDMASTER sortiert automatisch neue Wörter alphabetisch ein, so daß sich bei umfangreichen Listen nach jeder Eingabe eine kleine Verzögerung ergibt. Maximal kann eine Liste 1000 Wörter umfassen. Wer diese Grenze überschreiten will, muß die Dimensionierung des Arrays w$() in Zeile 100 und 980 erhöhen. Die Wortlänge sollte nicht mehr als sechs Buchstaben betragen, da sonst im Hauptprogramm Probleme mit der Anzeige auftauchen.
Nach der Ruckkehr ins Hauptmenue ist WORDMASTER hoffentlich gut gefüttert und zufrieden, es kann losgehen. Der gesamte Spielablauf findet im Dialog mit dem Programm statt, so daß eine umfangreiche Anleitung überflüssig ist. Wenn Sie sich entscheiden, die Partie zu beginnen, so müssen Sie zunächst ein Wort raten, das sich WORDMASTER ausgedacht hat. Neben der Eingabe Ihrer Versuche haben Sie jederzeit die Möglichkeit, mit den Cursotasten <oben> und <unten> die Wortliste zu durchsuchen, falls Ihnen nichts mehr einfällt. Im Notfall können Sie sich sogar durch Eingabe eines Fragezeichens das geheime Wort verraten lassen, doch dann werden Ihnen automatisch 10 Versuche angerechnet, und Sie haben die Runde mit großer Wahrscheinlichkeit verloren.
Falls Sie ein Wort eingeben, das WORDMASTER noch nicht kennt, so möchte das Programm wissen, ob das Wort neu in die Liste aufgenommen werden soll; nur in diesem Fall wird es als Versuch akzeptiert. Hüten Sie sich davor, unsinnige Buchstabenkombinationen zu verwenden, denn WORDMASTER paßt sich Ihrer Wortwahl an und benutzt die Eingabe bei nächster Gelegenheit womöglich als geheimen Code! Wenn das neu gewonnene Wissen erhalten bleiben soll, so muß natürlich nach Beendigung des Spiels die erweiterte Wortliste mit Punkt <4> des Hauptmenues neu abgespeichert werden. Auf diese Weise vergrößert das Programm mit jeder Spielrunde seine Wissensbasis.
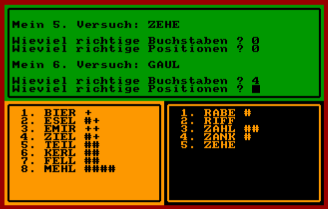
Ihre Versuche und Trefferquoten werden in einem separaten Bildschirmfenster protokolliert. Bemühen Sie sich auf jeden Fall, mit möglichst wenigen Versuchen auszukommen! Nachdem Sie das gesuchte Wort gefunden haben, ist WORDMASTER an der Reihe, und Sie dürfen sich ein geheimes Wort ausdenken. Wie Sie sehen werden, findet das Programm den Code meistens sehr schnell, und wenn es dabei weniger Versuche braucht, haben Sie die Runde verloren. Andererseits kann es natürlich passieren, daß WORDMASTER das Wort noch nicht kennt, und in ausgleichender Gerechtigkeit werden dann dem Programm 10 Versuche aufgebrummt. Allerdings lernt es auch in diesem Fall dazu!
Die Versuchsergebnisse für WORDMASTER bestehen aus zwei Zahlen (richtige Buchstaben/richtige Positionen). Falls Sie nach der ersten Eingabe <DEL> drücken, so kann diese korrigiert werden; <DEL> vor der ersten Eingabe führt zum Neubeginn des Ratevorgangs. Dieser Abbruch ist nur sinnvoll, wenn Sie einen Eingabefehler in einem vorherigen Versuch entdecken, der WORDMASTER natürlich daran hindert, den Code zu entschlüsseln. Unbemerkte Eingabefehler werden vom Programm im allgemeinem nach Beendigung der (erfolglosen) Suche gefunden und angezeigt.
WORDMASTER behält also auf jeden Fall die Übersicht, und wenn man sich anschaut, wie zielstrebig das geheime Wort ermittelt wird, so scheint das Programm in der Tat die vorhin beschriebene wissenschaftliche Stategie spielend zu bewältigen. Doch ehrlich währt am längsten: Gegen allen Anschein kann es weder logische Schlüsse ziehen noch Theorien aufstellen und überprüfen - das einzige, was WORDMASTER wirklich leistet, ist eine überzeugende Simulation dieser Fähigkeiten!
Wer sich an Kapitel 5 (Mit roher Rechengewalt) erinnert und die Anzeige des Denkvorgangs auf dem Bildschirm kritisch betrachtet, wird bald erkennen, daß hier nur ein schneller Such-Algorithmus am Werke ist... aber stop! Damit das Spiel noch eine Weile seinen Reiz behält, soll es diesmal ausnahmsweise Ihnen überlassen bleiben, das genaue Verfahren herauszufinden. Die Programmzeilen 2880 - 3090 dürften für eine ausgiebige Analyse einige Hinweise geben, die hier jedoch nicht mehr zur Sprache kommen können, da wir noch Platz für ein anderes heißes Thema brauchen:
Bevor Sie mit dieser Überschrift den Verdacht bestätigt finden, daß der Autor dieser Zeilen nun endgültig einem galoppierenden Größenwahn verfallen ist, hier ein kurzer Rückblick in die Geschichte der künstlichen Intelligenz, der alles erklärt: Zu Beginn der Computerära war der Optimismus trotz der nach heutigem Standard erbärmlichen Hardware ungebrochen, und in den fünfziger Jahren wurde allen Ernstes an Programmen gearbeitet, die nicht nur spezielle Aufgaben, sondern jedes beliebiges Problem lösen sollten. Und ob Sie es glauben oder nicht: Die Bemühungen hatten sogar Erfolg! 1957 entstand der in Fachkreisen berühmte General Problem Solver (GPS) von Newell, Shaw und Simon. Damit drängt sich natürlich die Frage auf, warum in aller Welt dieses Programm nicht eingesetzt wurde, um endlich die großen Probleme der Menschheit zu lösen - doch dazu kommen wir gleich. Zunächst soll in Grundzügen dargestellt werden, mit welchem Ansatz dieses softwaremäßige Universalgenie arbeitet.
Alle Problem entstehen im Prinzip aus einer Differenz zwischen einem gegebenen Ist-Zustand und einem erwünschten Soll-Zustand und lassen sich damit auf die Frage 'Wie komme ich von A nach B' reduzieren. Sie sind zu Hause, wollen aber gerne nach Honolulu, oder sind ledig und möchten heiraten, oder haben kein Geld, brauchen aber mindestens zwei Riesen für Ihren neuen Wunsch-PC... einen Moment, das werden wir gleich haben: In der Welt, auf die sich das Problem bezieht, gibt es im allgemeinen nützliche Objekte (Verkehrsmittel, Zeitschriften, Sparkassen) und dazu passende Operatoren (Taxi bestellen, Heiratsanzeige aufgeben, Bank überfallen), mit denen sich der Zustand A transformieren, d.h. in einen anderen Zustand überführen läßt.
Natürlich kann man nicht erwarten, daß ein einziger Operator sofort den gewünschten Zustand B herstellt, sondern es müssen oft ganze Ketten von Operatoren in der richtigen Reihenfolge angewendet werden. Doch keine Sorge, die findet der GPS schon heraus. Wir müssen dem Programm nur voher begreiflich machen, auf welche Weise welche Operatoren mit welchen Objekten auf welche Zustände wirken...
Sehen Sie - und genau deshalb hat sich der GPS nie durchsetzen können. Die Kodierung und Aufbereitung aller relevanten Daten ist nämlich so zeitaufwendig, daß sich der Beitrag des Programms zur Lösung des Problem dagegen sehr bescheiden ausnimmt, oder mit anderen Worten: Ohne Computer lassen sich die Probleme meist schneller lösen. Sinnvoll wäre der GPS nur, wenn er die Daten selbständig erfassen könnte, doch in dieser Hinsicht sind die Experten heute sehr pessimistisch. Alles in allem muß das Projekt deshalb als Fehlschlag bezeichnet werden, hat aber trotzdem der gesamten KI-Forschung wesentliche Impulse vermittelt. Außerdem ist die Idee einfach zu interessant, um sie hier unter den Tisch fallen zu lassen. Eine Demonstration der GPS-Arbeitsweise auf einem CPC ist nun zwar etwas zu hoch gegriffen - hier wäre endgültig der Umstieg auf PROLOG fällig - doch wie sieht es mit einem speziellen Problemlöser aus, der zumindest im Ansatz einige der Ideen verwirklicht? Zu diesem Zweck kommen uns die WORDMASTER-Wortlisten wie gerufen:
Vermutlich haben Sie den folgenden Aufgabentyp schon einmal in der Rätselecke einer Illustrierten gesehen:
GERD .... .... .... WOLF
In jeder Vollmondnacht verwandelt sich Gerd unweigerlich in einen Wolf - wie geht das vor sich? Es wird jeweils ein Buchstabe ausgetauscht, so daß ein neues gültiges Wort (aus der Liste) entsteht, und damit wären bereits die Operatoren für unser Problem definiert. Als Differenz zwischen dem Ist- und dem Soll-Zustand kann die Anzahl der unterschiedlichen Buchstaben gelten. Da die Differenz zu Beginn vier Buchstaben beträgt und die Aufgabe in vier Schritte gelöst werden soll, ist klar, daß jede Umwandlung die Differenz um 1 reduzieren muß; aus diesem Grund ist die Aufgabe auch nicht besonders schwierig.
Wesentlich härtere Probleme bringt jedoch eine andere Transformation mit sich, die in der Realität recht häufig vorkommt, nämlich die Umwandlung von GELD in BIER. Durch Probieren kann man sich davon überzeugen, daß sich die Differenz auf Anhieb nicht verringern läßt, da keiner der Buchstaben aus BIER in GELD hineinpaßt, d.h. zu einem existierenden Wort führt. Mit Sicherheit brauchen wir mehr als vier Schritte und müssen uns auf Umwege einlassen. Wieviel Schritte werden also mindestens notwendig sein? Diese Frage ist nicht ohne weiteres zu beantworten. Bekannt ist bisher eine Lösung, die sechs Zwischenstationen erfordert. Sie beginnt mit der Umwandlung von GELD in HELD - versuchen Sie mal, den Rest zu finden! Sehr behilflich war dem Autor dabei ein kleines Programm, das eine der WORDMASTER-Listen nach vierbuchstabigen Wörtern durchsucht, die sich von dem eingegebenen Wort genau in einem Buchstaben unterscheiden.
10 OPENOUT "X": MEMORY HIMEM-1: CLOSEOUT 20 OPENIN "LISTE4.DAT" 30 a=0: DIM w$(1000) 40 WHILE NOT EOF: a=a+1: INPUT#9,w$(a): WEND 50 CLOSEIN 60 INPUT "Wort: ",a$: a$=UPPER$(a$) 70 FOR i=1 TO a 80 dif=0 90 FOR j=1 TO 4 100 IF MID$(a$,j,1) <> MID$(w$(i),j,1) THEN dif=dif+1 110 NEXT j 120 IF dif=1 THEN PRINT w$(i);" 130 NEXT i 140 PRINT: PRINT: GOTO 60
Die Arbeit mit diesem Programm ist sehr aufschlußreich, da sie einiges über die Struktur der Wortliste verrät. Es gibt hier Inseln, also einzelne Wörter (z.B. AUTO) und kleine Wortgruppen, die keine weitergehende Transformation zulassen, oder auch Sackgassen, d.h. Wörter, die nur einen einzigen Umwandlungspartner haben und keine Verkettung in mehrere Richtungen erlauben. Die Liste erscheint unter diesem Aspekt als eine Art Wortlabyrinth, durch das sich der bierdurstige Forscher mühsam hindurchtastet. Sicherlich läßt sich damit eine neue und interessante Spielidee entwickeln, doch bleiben wir bei unserem Problemlöser: Gesucht ist ein Programm, das a) Augaben dieser Art löst, und b) Aufgaben dieser Art konstruiert!
Wenn wir es bei einfachen Aufgaben mit vier Schritten (siehe Gerd, der Werwolf) belassen, so scheint solch ein Programm zwar nicht unbedingt trivial, aber immerhin realisierbar zu sein, da mit der Reduzierung der Buchstabendifferenz eine klare Bedingung für jeden Schritt vorliegt. Haarig wird es jedoch bei unserem GELD-BIER-Problem: Was soll hier der Suche eine Richtung geben? Wie kann ein Programm Inseln und Sackgassen erkennen, Endlosschleifen verhindern?
Diese offenen Fragen wurden in der Ausgabe 1/87 von PC International an die Leser weitergereicht, in der Hoffnung, daß der eine oder andere versierte Datenbastler zumindest eine Teilantwort finden würde. Und die Reaktion übertraf in der Tat alle Erwartungen: Lesen Sie im nächsten Kapitel, was geschah...