Das erklärte Ziel der künstlichen Intelligenz ist die Simulation menschlicher Denkvorgänge. Doch ob sich dieses Ziel erreichen läßt, darüber streiten sich die Gelehrten. Sicherlich hat die KI-Forschung schon einige Teilerfolge vorzuweisen, doch unerreicht ist bis heute die ungeheure Flexibilität und Vielseitigkeit des menschlichen Denkens. Alle existierenden angeblich intelligenten Programme beherrschen nur ein sehr begrenztes Wissensgebiet, und der Schachcomputer, mit dem man sich nebenbei über Gott und die Welt unterhalten kann, wird wohl noch einige Zeit auf sich warten lassen.
Aber selbst bei einem Programm, das die Fähigkeiten eines menschlichen Experten erreicht oder sogar übertrifft, sind Zweifel angebracht, ob es sich dabei wirklich um eine intelligente Leistung handelt. Diesen Zweifel entwickelt im allgemeinen weniger der Anwender, der ja nur die Ergebnisse zu sehen bekommt, sondern vielmehr der Programmierer, der seiner Maschine Byte für Byte beibringen muß, wie das Problem gelöst wird. Er weiß, daß die eindrucksvollen Ergebnisse oft nur durch relativ simple Prozeduren erzielt werden, die in irgendwelchen Schleifen mit einem Affenzahn einige hundert Male durchlaufen werden - was hat das mit Intelligenz zu tun?
Auch wenn ein Mensch und eine Maschine bei einer Aufgabe zum gleichen Ergebnis kommen, so ist doch die Methode meist unter schiedlich. Dazu gleich ein Beispiel: Wie würden Sie an das folgende Problem herangehen (ohne Computer)?
Gesucht sind zwei zweistellige ganze Zahlen, deren Produkt 999 beträgt.
Offenbar ist eine gewisse Portion Intelligenz notwendig, um diese Aufgabe ohne überflüssige Rechnerei zu lösen. In der Tat existiert eine einfache Methode, mit der man das Ergebnis sehr schnell ermitteln kann... verraten wird sie hier natürlich nicht! Falls Sie zu den Auserwählten gehören, die das Verfahren auf Anhieb entdecken, seien Sie nicht allzu deprimiert, wenn der CPC das Ergebnis Ihrer Intelligenzleistung ebenfalls in Sekundenschnelle findet, und zwar mit einem ziemlich primitiven Vierzeiler:
10 FOR x% = 10 TO 99 20 FOR y% = 10 TO 99 30 IF x%*y% = 999 THEN PRINT x%; y%: END 40 NEXT y%, x%
Zwar verbringt der Computer hier die meiste Zeit mit vollkommen unsinnigen Berechnungen, doch die hohe Ablaufgeschwindigkeit macht diesen Nachteil mehr als wett. Das Problem wird einfach mit roher Rechengewalt gelöst, und nicht umsonst hat dieser Programmtyp in der Fachliteratur den Beinamen Brute Force erhalten.
Dieses Beispiel zeigt jedenfalls deutlich, daß die Leistungen von Menschen und Maschinen auf vollkommen verschiedenen Voraussetzungen beruhen. Der menschliche Verstand ist vergleichsweise langsam, aber vielseitig; Computer sind ungeheuer stur, dabei jedoch sehr schnell und präzise. Eine effektive Methode zur Problemlösung muß natürlich diesen unterschiedlichen Hardwareeigenschaften gerecht werden. Auch im Bereich der strategischen Spiele spiegelt sich dieser Unterschied wieder. Programme, die nach der menschlichen Methode vorgehen, untersuchen nur eine kleine Auswahl sinnvoller Züge, müssen jedoch sehr viel strategisches Wissen enthalten und es vor allem korrekt anwenden. Die Spielstärke hängt sehr stark davon ab, wie differenziert das Programm, bei der Analyse vorgeht: Es muß in der Lage sein, eine große Anzahl verschiedener Stellungstypen und Merkmale zu unterscheiden, um ihre Bedeutung im Gesamtzusammenhang richtig einzuschätzen.
Doch wie bereits im letzten Kapitel angedeutet, bringt die Programmierung einer vielseitigen Bewertungsfunktion erhebliche Problem mit sich. Wer versucht hat, das Gobang-Programm durch veränderte Parameter zu verbessern, kann davon sicherlich ein Lied singen: Wie man es auch dreht und wendet - es finden sich immer wieder Situationen, in denen die Zugbewertung nicht greift, d.h. wichtige Tatsachen falsch einschätzt oder einfach übersieht. Eine verfeinerte und damit aufwendigere Bewertungsfunktion könnte zwar in einigen Fällen Abhilfe schaffen, stellt aber den Programmerer vor sehr komplizierte Aufgaben und verlängert natürlich auch die Rechenzeit.
Trotz intensiver Bemühungen ist es bis heute nur ansatzweise gelungen, eine menschliche Vorgehensweise mit ausreichender Effektivität auf einen Computer zu übertragen. Deshalb werden wir uns in diesem Kapitel mit einem anderen Programmtyp beschäftigen, dessen Leistungsfähigkeit mehr auf der Rechengeschwindigkeit beruht als auf feinsinnigen Analyseverfahren - und es ist in der Tat erstaunlich, welche 'Intelligenz' ein kleiner Z 80-Prozessor mit 4 MHz Taktfrequenz entwickelt, wenn er so richtig loslegen darf! Als Demonstrationsobjekt wird uns diesmal ein Spiel dienen, das zur Abwechslung nicht aus Asien, sondern aus Afrika stammt.
Für eine Partie Kalaha braucht man 72 Bohnen und 14 Töpfe. Zu Beginn liegen sechs Bohnen in jedem Topf, nur die beiden Sammeltöpfe an der linken und rechten Seite bleiben leer. Jeder der beiden Spieler hat Zugriff auf die sechs Töpfe, die sich auf seiner Seite befinden. Gezogen wird, indem man aus einem seiner Töpfe die Bohnen entnimmt und sie auf die nachfolgenden Töpfe reihum im Gegenuhrzeigersinn verteilt. Beginnt zum Beispiel der Rechner mit seinem fünften Topf (obere Reihe, von rechts gezählt), so liegen danach in seinem sechsten Topf sieben Bohnen, in seinem Sammeltopf eine Bohne und in den Töpfen 1..4 des Gegners (untere Reihe, von links gezählt) jeweils sieben Bohnen.

Dazu kommen noch zwei Sonderregeln.
Ansonsten wird abwechselnd gezogen. Gewonnen hat, wer zuerst mehr als 36 Bohnen in seinen Sammeltopf gebracht hat. Falls ein Spieler nicht mehr ziehen kann, weil seine Töpfe alle leer sind, so hat er verloren. Aus dem Sammeltopf kann nicht gezogen werden, die dort befindlichen Bohnen liegen fest.
Nach dem Start des Programms KALAHA.BAS möchte der Rechner zunächst die gewünschte Spielstufe wissen - je höher die Stufe, um so stärker spielt das Programm, benötigt dafür allerdings auch mehr Rechenzeit. Durch eine weitere Eingabe bestimmen Sie, wer die Partie beginnt. Falls Sie am Zug sind, erscheint ein Pfeil auf dem Bildschirm, der durch die Cursortasten <links> und <rechts> gesteuert wird. Durch Drücken von <ENTER> bzw. <RETURN> können Sie den Topf anwählen, aus dem Sie ziehen wollen, der Rechner verteilt danach die Bohnen reihum. Auch wenn das Programm seinen Zug ermittelt hat, erscheint zunächst ein Pfeil, der den entsprechenden Topf markiert. Erst nach <ENTER> wird der Zug ausgeführt, so daß Sie sich in Ruhe anschauen können, was Ihr elektronischer Spielpartner sich da ausgedacht hat. Nach Abschluß der Partie startet eine beliebige Taste ein neues Spiel.
Ihre ersten Versuche unternehmen Sie am besten in der ersten oder zweiten Spielstufe, um nicht gleich zu Beginn demoralisiert zu werden. Bereits in der dritten Stufe reagiert das Programm ausgesprochen ungemütlich und ist ab Stufe 6 nur noch sehr schwer zu schlagen. Auch wem man die Partie eine Zeit lang ausgeglichen halten kann, findet der Rechner irgendwann raffinierte Zugkombinationen, die ihn deutlich in Vorteil bringen - und spätestens hier wird jeder Programierfreak neugierig, wie diese Intelligenzleistung zustande kommt.
Einen kleinen Hinweis liefert immerhin die Anzeige der Stellungsbewertung in der linken oberen Bilschirmecke: Die erste Zahl gibt während des Suchvorgangs den bislang besten Zug an, die zweite Zahl den dazugehörigen Erwartungswert. Bei einem positiven Wert sieht sich das Programm im Vorteil, bei einem negativen Wert im Nachteil, und der Wert 0 deutet auf eine ausgeglichene Stellung hin. Falls eine Bewertung von +99 erscheint, so hat der Rechner einen sicheren Gewinnweg entdeckt, bei -99 sieht er dagegen keine Chance mehr und gibt auf.
Wie Sie aus dem Listing ersehen können, wird die Zugberechnung durch ein Maschinenprogramm vorgenommen. Den Datazeilen kann man natürlich nicht mehr ansehen, wie das Programm dabei vorgeht. Deshalb werden wir es jetzt durch eine BASIC- Routine ersetzen, die zwar längst nicht so leistungsfähig ist, dafür aber anschaulich das Prinzip demonstriert. Gehen Sie zu diesem Zweck auf folgende Weise vor:
Die aus dem Hauptprogramm entfernte Zeile 1140 sorgt normalerweise für die Einhaltung der Sonderregel (2). Die folgenden Betrachtungen werden jedoch wesentlich verständlicher, wem beide Spieler streng abwechselnd ziehen. In Kauf nehmen müssen wir dabei, daß Kalaha ohne diese Regel einiges an Spielwitz einbüßt. Wer also nur spielen will, ist mit der Grundversion besser beraten.
Für das Verständnis der folgenden Ausführungen ist es sehr günstig, wenn Ihnen ein Listing der Basic-Zugberechnung vorliegt. Sie können es mit LIST 5000- auf dein Bildschirm bzw. mit LIST 5000-,#8 auf dem Drucker ausgeben lassen.
Wie ein erster Versuch zeigt, spielt die BASIC-Version V1 zwar ausgesprochen schwach (die Eingabe der Spielstufe ist hier ohne Bedeutung), doch dafür ist die Vorgehensweise sehr leicht zu durchschauen: Alle möglichen Züge des Rechners (maximal 6) werden probeweise ausgeführt und danach die Differenz aus der Anzahl der Bohnen im Sammeltopf des Rechners und des Gegners gebildet - je größer das Ergebnis, um so besser der Zug. Da diese Zugbewertung einem ausgeglichenen Spielstand den Wert 0 zuordnet, handelt es sich im Gegensatz zu der GobangBewertungsfunktion im letzten Kapitel um eine symmetrische Funktion
Das Spielfeld wird intern durch das Array in(14,9) repräsentiert. Die Variablen in(1,0)...in(14,0) enthalten die Anzahl der Bohnen, wobei der Gegner die Töpfe 1...6 und der Rechner die Töpfe 8...13 belegt; Nr. 7 und Nr. 14 sind die Sammeltöpfe. Da wir noch einige Hilfsspielfelder benötigen, wurde das Array mit einem zweiten Index versehen, also mehrstöckig aufgebaut. Mit diesen Informationen und einigen ergänzenden Kommentaren sollte das Listing keine Rätsel mehr aufgeben.
Zeile 5020: Die Bewertung wird mit -99 initialisiert, dem denkbar schlechtesten Ergebnis. Sie bleibt erhalten, falls das Programm keinen legalen Zug findet, und signalisiert in diesem Fall dem Hauptprogramm, daß es an der Zeit ist, aufzugeben.
Zeile 5040: Falls der Topf, aus dem gezogenen werden soll, leer ist, so werden die folgenden Schritte übersprungen.
Zeile 5050-5080: Um den Zug auszuführen, wird das Spielfeld auf ein Hilfsspielfeld kopiert und bei dieser Gelegenheit umgedreht. Durch die vertauschten Seiten erhält der Rechner passen zur FOR...NEXT-Schleife die Topfnummern 1...6. Eine Laufvariable von 8...13 würde es zwar auch tun, aber da wir dieses Verfahren für die kommenden Versionen ohnehin brauchen, wird es der Einfachheit halber schon jetzt eingeführt.
Zeile 5090-5140: Hier wird der Zug ausgeführt. Die Bohnen werden dem Topf entnommen, in die Variable anz (Anzahl) übertragen und durch die FOR...NEXT-Schleife auf die folgenden Töpfe verteilt.
Zeile 5150: Falls die letzte Bohne in einen eigenen leeren Topf gefallen ist, wird die Sonderregel (1) durchgeführt.
Zeile 5160: Züge die zum Gewinn des Gegners führen, werden übergangen.
Zeile 5170-5180: Der Zug wird bewertet und in der Variablen bestzug notiert, falls er das bislang beste Ergebnis übertrifft.
Solch eine einfache Zugbewertung hat natürlich den Vorteil, daß sie sehr schnell berechnet werden kann. Nur macht sich immer wieder katastrophal bemerkbar, daß die Antwort des Gegners in keiner Weise berücksichtigt wird. Was nützt ein stolzes Ergebnis von +3, wenn der Gegenzug die Bewertung auf -10 herabdrückt? Diese Art von Kurzsichtigkeit, in der Fachliteratur auch als Horizonteffekt bekannt, läßt sich durch eine statische Zugbewertung nur schlecht vermeiden. Nötig ist deshalb eine dynamische Bewertung, bei der auch die Gegenzüge probeweise ausgeführt werden.
Wie wird eine solche dynamische Methode nun in der Praxis realisiert? Anstelle der Zugbewertung muß in Zeile 5170 ein weiteres Unterprogramm aufgerufen werden, das den besten Gegenzug ermittelt. Der Gegner wird natürlich versuchen, möglichst wenige Bohnen in den Sammeltopf des Rechners zu bringen, aber dafür den eigenen Sammeltopf so weit es geht füllen. Wenn wir wie gehabt die Differenz zwischen diesen beiden Werten heranziehen, ist der beste Zug des Gegners genau der, bei dem die Bewertung minimal wird. Der Spielbaum im folgenden Diagramm verdeutlicht das Verfahren.
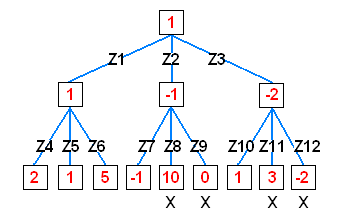
Angenommen wird dabei, daß dem Rechner und seinem Gegner jeweils drei Zugmöglichkeiten zur Verfügung stehen. Wenn der Rechner den Zug Z1 auf der linken Seite ausführt, müssen die Antworten Z4...Z6 überprüft werden, und wie aus dem Diagramm ersichtlich wird, kann der Gegner die Bewertung höchstens auf 1 herabdrücken. Dieses Minimum stellt auch gleichzeitig den Wert des Rechnerzugs dar, die Bewertung wird also quasi in die vorherige Ebene heraufgereicht.
Wählt der Rechner den Zug Z2, so kann in einer der Varianten sein Vorsprung sogar auf 10 Bohnen hochschnellen - doch das Risiko ist zu hoch: Ein versierter Gegner wird natürlich mit Z7 antworten und sich damit einen Vorsprung von einer Bohne sichern. Die endgültige Bewertung für den Zug Z2 beträgt also -1, und damit ist er trotz der verführerischen Aussicht von +10 effektiv schlechter als der Zug auf der linken Seite. Das Programm sucht also letztendlich das Maximum der heraufgereichten Minima , wodurch klar wird, warum dieses Verfahren kurz und bündig den Namen Minimax erhalten hat.
Ohne Zweifel wird ein Programm mit dieser Methode besser spielen als mit der kurzsichtigen statischen Bewertung. Im Auge behalten muß man jedoch, daß die statische Bewertung nicht aufgehoben, sondern nur aufgeschoben wurde. Wenn das Programm auf diese Weise den besten Zug seines Gegners ermittelt, ist also nach unseren bisherigen Erfahrungen nicht unbedingt sicher, ob es sich wirklich um den besten Zug handelt. Die Gefahr von Fehleinschätzungen ist zwar vermindert, aber noch längst nicht beseitigt! Doch was hindert uns daran, auch die beste Antwort auf den Zug des Gegners mit der dynamischen Minimax-Methode zu berechnen? Wir müssen ja nur den Spielbaum um eine weitere Stufe ergänzen, in der die möglichen Antworten das Rechners ausprobiert werden. Dazu benötigen wir eine weitere Unterprogrammebene, in der nach bewährtem Schema wiederum der optimale Zug des Rechners (und das dazugehörige Maximum gesucht wird. Doch damit noch nicht genug: Auch diesen Zug könnte man wieder dynamisch ermitteln...
Doch um es kurz zu machen: Theoretisch ist mit dem Minimax-Verfahren zwar eine Untersuchung des kompletten Spielbaumes bis zum Spielende möglich, doch in der Praxis wird dieses Vorhaben durch die explosionsartig anwachsende Anzahl der Verzweigungen in den tieferen Ebenen verhindert. Wenn man annimmt, daß in einer Kalaha-Partie durchschnittlich fünf Zugmöglichkeiten vorhanden sind, so erfordert eine Minimax-Analyse bis zur n-ten Ebene die Bewertung von 5n Endpositionen. Eine Vorausberechnung von 12 Zügen (sechs für den Rechner und sechs für den Gegner) erzeugt bereits 244 Millionen Endstellungen, und hier tauchen selbst für sehr leistungsfähige Computer unüberwindliche Grenzen auf. Dabei ist der Verzweigungsfaktor bei Kalaha noch vergleichsweise harmlos: In Schachstellungen sind z.B. durchschnittlich 40 verschiedene Züge möglich.
Auch wenn die Maschine noch so schnell ist - irgendwo muß also eine Grenze gesetzt und die Stellung statisch abgeschätzt werden. Klar ist jedoch, daß ein Programm um so stärker spielt, je weiter es mit seiner Analyse im Spielbaum vordringt. Natürlich steigt damit auch die Rechenzeit an, oder anders gesagt: Die Spielstärke bei einem vorgegebenen Zeitlimit hängt unmittelbar von der Geschwindigkeit des Computers ab.
Wie wird die Minimax-Baumsuche nun programmtechnisch realisiert? Zunächst scheint es so, als müßte man für jede Ebene ein separates Unterprogramm schreiben, wobei erst das letzte die statische Bewertung durch Differenzbildung vornimmt. Doch der versierte Programmierer erkennt sofort, daß diese Unterprogramme alle sehr ähnlich aussehen, und fragt sich natürlich, ob man nicht auch mit einer einzigen Subroutine auskommen könnte, die sich dann schlauerweise selbst aufruft.
In der Tat existiert ein als Rekursion bekanntes Verfahren, mit dem sich dieses Problem sehr elegant lösen läßt Obwohl die Grundvoraussetzung für rekursive Programmstrukturen - nämlich die Möglichkeit verschachtelter GOSUBs - in BASIC gegeben ist, tauchen hier jedoch einige Schwierigkeiten auf. Schauen Sie sich zunächst die folgende stark vereinfachte Struktur an:
100 st=st+1 110 FOR zug=1 TO 6 120 'Spielfeld kopieren' 130 'Seiten vertauschen' 140 'Zug ausführen' 150 IF st=stmax THEN 'statistische Bewertung' ELSE GOSUB 100: 'dynamische Bewertung' 160 IF 'neuer Bestwert' THEN 'Zug und Bestwert merken' 170 NEXT zug 180 st=st-1: RETURN
Hier wurde vorsorglich eine Abbruchbedingung eingebaut: Sobald die Suchtiefe st eine vorgegebene Grenze stmax erreicht, nimmt das Programm die endgültige Bewertung vor und beendet die Rekursion. Natürlich muß die Variable st bei jedem Aufruf um 1 erhöht und jedem RETURN um 1 erniedrigt werden, damit das Programm jederzeit weiß, auf welcher Ebene es sich gerade befindet. Weiterhin wird an dieser Stelle deutlich, welchen Vorteil der Programmteil Seiten vertauschen bietet: Er sorgt automatisch dafür, daß immer abwechselnd Züge des Rechners und des Gegners ausgeführt werden, so daß wir für beide Seiten mit einem Unterprogramm auskommen.
Ärger wird es jedoch mit der Schleifenvariablen zug geben, da sie nach jedem GOSUB 100 neu initialisiert wird und damit den Zählerstand auf der vorherigen Ebene durcheinanderbringt. Hier macht sich unangenehm bemerkbar, daß BASIC, im Gegensatz zu Pascal oder LOGO, keine lokalen Variablen kennt, die trotz Namensgleichheit eindeutig nur einem Unterprogramm bzw. einer Unterprogrammebene zugeordnet sind. Ähnliche Überlegungen gelten übrigens für die Variablen bestwert und bestzug: Auch hier braucht jede Ebene ihre eigene Schublade.
Was also tun? Die erste Idee ist natürlich, ein Array zug(st) zu benutzen,
110 FOR zug(st) = 1 TO 6
und das sieht zwar sehr schön aus, funktioniert aber leider nicht, da das Locomotive-Basic keine indizierten Variablen in FOR... NEXT-Schleifen gestattet: Syntax Error! Glücklicherweise steht uns mit WHILE...WEND noch eine andere Schleifenkonstruktion zur Verfügung, die das Problem zwar nicht ganz so elegant löst, aber dafür indizierte Variablen akzeptiert:
105 zug(st) = 6 110 WHILE zug(st) > 0 : : : 165 zug(st) = zug(st) - 1 170 WEND
Doch jetzt genug der grauen Theorie! Das Unterprogramm Zug Computer V2 realisiert alle bisher erläuterten Ideen; Sie können es mit MERGE "ZUGCOMV2" anstatt der alten V1-Version in das Programm integrieren. Auch hier sollten Sie sich mit LIST 5000-,#8 einen Ausdruck erzeugen, damit die folgenden Ausführungen verständlich werden.
Die maximale Suchtiefe stmax wird durch die Eingabe der Spielstufe nach dem Programmstart bestimmt; allerdings sollten Sie zunächst keinen höheren Wert als 3 vorgeben, da sonst die Rechenzeit ungemütlich lang wird. In der Spielstufe 1 spielt das Programm zwar genauso schwach wie die Version V1, doch schon in der zweiten Stufe ist eine deutliche Steigerung zu bemerken: Der Rechner stolpert nicht mehr in jede Falle, da ihn die Vorausberechnung des Gegenzuges meist schon verrät, was Sie im Schilde führen. In der dritten Stufe erweist er sich schließlich als recht zäher Gegner, und man muß sich schon anstrengen, um noch zu gewinnen.
Die Struktur des neuen Programm-Moduls entspricht weitgehend der Version V1. Dazu noch ein paar ergänzende Hinweise:
Zeile 5020-5050: Dieser Vorspann initialisiert die Suchtiefe st mit 0, ruft das eigenliche rekursive Unterprogramm auf und organisiert die Variablenübergabe an das Hauptprogramm.
Zeile 5110-5140: Das Spielfeld wird kopiert und umgedreht. Natürlich hat jede Ebene ihr eigenes Hilfsspielfeld in(topf,st).
Zeile 5150-5210: Der Zug wird ausgeführt.
Zeile 5230: Nach dem rekursiven Aufruf wird die Bewertung des besten Zuges von der nächsttieferen Ebene übernommen. Da das Umdrehen des Spielfeldes auch die beiden Sammeltöpfe vertauscht, erscheint die Bewertung mit einem falschen Vorzeichen, was korrigiert werden muß.
Zeile 5240: Zunächst verwirrt hier, daß entgegen dem Minimax-Prinzip auch bei Zügen des Gegners scheinbar ein Maximum gesucht wird. Da jedoch, wie gesagt, bei jedem rekursiven Aufruf das Vorzeichen der Bewertungsdifferenz in(7,st) - in(14,st) umgedreht wird, ist das Maximum auf jeder zweiten Suchebene in Wirklichkeit ein Minimum... als ob es nicht schon kompliziert genug wäre, mag mancher Leser hier bemängeln - aber die elegante Lösung mit nur einem Unterprogramm hat eben ihren Preis. Zum Verständnis der ganzen Angelegenheit trägt jedenfalls die Anzeige der aktuellen Suchtiefe in der linken oberen Bildschirmecke bei: Hier können Sie beobachten, wie das Programm im Spielbaum herumklettert.
Ein großer Nachteil des Minimax-Verfahrens ist leider das starke Anwachsen der Rechenzeit mit jeder zusätzlichen Suchebene. Bereits in Stufe 4 wird sie unerträglich lang. Deshalb soll noch ein ergänzendes Verfahren vorgestellt werden, das es auf überraschend einfache Weise ermöglicht, große Bereiche des Spielbaumes zu ignorieren und trotzdem das gleiche Ergebnis wie bei einer vollständigen Suche zu erhalten.
Werfen wir zu diesem Zweck noch einmal einen Blick auf das Bild, das den Spielbaum darstellt. Nachdem das Programm den Zug Z1 mit allen Konsequenzen durchgerechnet hat, erwartet es also zumindest einen Wert von +1 und notiert sich das Ergebnis in der Variablen bestwert(1). Danach wird Z2 untersucht, und bereits die Betrachtung des ersten Gegenzuges Z7 stellt klar, daß der Gegner auf jeden Fall das Ergebnis -1 erreichen kann. Da wir ja aus dieser Ebene das Minimum der Bewertungen nach oben übertragen, wird die Bewertung durch die Untersuchung der weiteren Gegenzüge Z8 und Z9 vielleicht noch schlechter, aber mit Sicherheit nicht besser werden.
Der aus der Untersuchung von Z1 stammende Erwartungswert kann also durch Z2 nicht übertroffen werden, und da diese Tatsache bereits nach der Bewertung des Gegenzuges Z7 feststeht, können die Züge Z8 und Z9 mitsamt allen weiterten Verzweigungen ignoriert werden, was in dem Diagramm durch ein X angedeutet wird. Für den Zug Z3 gelten ähnliche Überlegungen: Zwar wird der Erwartungswert durch Z10 erreicht, aber nicht verbessert, so daß auch hier weitere Varianten keine Rolle mehr spielen - es sei denn, man möchte das Programm zwischen gleichwertigen Zügen nach einem Zufallsprinzip wählen lassen.
De Erwartungswert für Züge des Rechners wird im allgemeinen mit dem griechischen Buchstaben Alpha bezeichnet; er entspricht unserem bestwert(st) bei ungeradzahligem st. Ein Zug gilt als wiederlegt, wem Alpha durch die Bewertung eines Gegenzuges unterboten wird; das Abschneiden der weiteren Gegenzüge wird Alpha-Cutoff genannt. Entsprechend läßt sich dieses Verfahren auch auf die dynamische Bewertung der Gegenzüge übertragen: Der Erwartungswert für den Gegner wird mit Beta bezeichnet, und der Cutoff erfolgt, falls die Antwort des Rechners diesen Wert überbietet (der Gegner sucht ja ein Minimum!).
Trotz dieser komplizierten Überlegungen ist erstaunlich wenig Aufwand nötig, um den Alpha-Beta-Algorithmus in unser Programm einzubauen. Ergänzen Sie im Unterprogramm Zug Computer V2 die folgenden Zeile:
5245 IF -wert <= bestwert(st-1) THEN zug(st) = 0
Durch Herabsetzen des Zugzählers auf 0 wird die WHILE...WEND-Schleife bei nächster Gelegenheit verlassen, alle weiteren Züge bleiben unberücksichtigt. Auch hier muß natürlich der durch das Umdrehen des Spielfeldes erzeugte Vorzeichenwechsel beachtet werden. Weiterhin besteht die Gefahr, daß das Programm in der ersten Ebene (st=1) auf den nicht definierten bestwert(0) zugreift. In der ersten Ebene dürfen natürlich keine Züge abgeschnitten werden, was durch die folgende Ergänzung zuverlässig verhindert wird:
5020 st = 0: bestwert(0)= -99
Nach erneutem Programmstart können sie anhand der Tiefenanzeige beobachten, wie große Bereiche des Spielbaumes übergangen werden, wodurch das Programm erheblich schneller wird. Sogar die Stufe 4 bietet jetzt erträgliche Rechenzeiten. Erwähnt werden muß allerdings noch, daß die Effektivität des Alpha-Beta-Algorithmus stark von der Reihenfolge abhängt, in der die Züge untersucht werden. Je eher der beste Zug auftaucht, um so mehr kann der Spielbaum reduziert werden. Wenn z.B. in dem im Diagramm dargestellten Spielbaum die Suche von rechts nach links erfolgt, so erhalten wir keinen einzigen Cutoff! Aus diesem Grund werden die Züge bei vielen Programmen zunächst einmal durch eine relativ flache Suche abgeschätzt und dann vorsortiert, bevor die eigentliche Analyse beginnt - eine der vielen Verfeinerungen der Minimax-Methode, mit denen man problemlos ein ganzes Buch füllen könnte.
In diesem Kapitel müssen wir uns jedoch auf die wesentlichen Grundlagen beschränken, die praktisch bei allen strategischen Spielprogrammen eine Schlüsselrolle einnehmen. Immerhin vermitteln die vorgestellten Beispiele in BASIC eine deutliches Bild von der Funktionsweise des Kalaha-Maschinenprogrammes, wenn auch die Sonderregel 2 noch einige besondere Tricks erfordert, die hier leider nur angedeutet werden können: Wenn ein Spieler noch einmal am Zug ist, wird das Spielfeld natürlich beim Aufruf der nächsten Ebene nicht umgedreht, und auch der Vorzeichenwechsel der Bewertungsfunktion entfällt. Weiterhin darf in diesem Fall auch kein Alpha-Beta-Schnitt erfolgen... alles etwas kompliziert, aber machbar! Zusätzlich wurde das Maschinenprogramm noch durch einen Zufallsgenerator ergänzt, der bei gleichwertigen Zügen die Entscheidung trifft und für Abwechslung sorgt.
Die BASIC-Versionen der Zugberechnung wurden geschrieben, um Ihnen Material in die Hände zu geben, mit dem Sie nach Herzenslust experimentieren können. Scheuen Sie sich also nicht, Veränderungen vorzunehmen und eigene Ideen auszuprobieren: Nur durch die Praxis gewinnt man die nötige Erfahrung, um selbst 'intelligente' Programme zu schreiben.