
Simulationen - Nachbildungen der Wirklichkeit - haben sich einen festen Platz unter den Standardanwendungen für Computersysteme erobert. Sei es bei der Ausbildung von Piloten für die Luft- oder Raumfahrt, bei wissenschaftlichen Forschungsprojekten oder in der wirtschaftlichen und militärischen Planung: In vielen Bereichen sind sie überhaupt nicht mehr wegzudenken.
Warum bisher keine Computersimulation die verantwortlichen Politiker und Militärs davon überzeugen konnte, wie gefährlich und unsinnig das Wettrüsten ist, sei allerdings dahingestellt. In dieser Folge des Software-Experiments werden wir uns mit einem anderen Thema beschäftigen, das ebenfalls sehr aktuell ist. Bereits in der letzten Folge wurde mit dem Game of Life ein Programm vorgestellt, das ansatzweise ein ökologisches System simuliert; und diese Idee soll noch etwas weiter verfolgt werden.
Bisher haben menschliche Eingriffe in die außerordentlich komplexe Dynamik ökologischer Systeme immer wieder zu der Erfahrung geführt, daß die Ergebnisse oft ganz anders aussehen, als es eigentlich geplant war. Insbesondere die langfristigen Folgen von zunächst sehr erfolgversprechenden Maßnahmen führen uns vor Augen, daß letztendlich der Mensch selbst betroffen ist, wenn er das empfindliche Gleichgewicht der Natur durch unbedachte Eingriffe zerstört. Der Einsatz von chemischen Mitteln verbessert die Ernteerträge - so sieht es in der Tat zunächst aus. Doch wenn sich nach einiger Zeit die bekämpften Schädlinge als resistent erweisen, ihre natürlichen Feinde dagegen scharenweise an dem Gift zugrunde gehen und die gesundheitlichen Folgen der Rückstande in den Nahrungsmitteln für den Menschen nicht mehr zu verantworten sind - was dann?
Die Dynamik ökologischer System wird durch eine Vielzahl ineinandergreifender Regelkreise und sich überlagernder Einflüsse bestimmt. Es ist deshalb kaum möglich, die Folgen von Eingriffen durch einfache, kausale Wenn-Dann-Modelle zu erfassen. Was liegt also näher, als sich mit Hilfe von Computersimulationen einen Einblick in dieses so wohlgeordnete Chaos zu verschaffen? Die Geschwindigkeit und Speicherkapazität moderner Rechenanlagen erlaubt es, Entwicklungen, die sich in der Realität über Jahre und Jahrzehnte erstrecken, in wenigen Sekunden ablaufen zu lassen und dabei durch gezielte Veranderung der Systemparameter eine ganze Palette von Möglichkeiten zu erforschen.
Doch dabei ist Vorsicht geboten: Ein Abbild der Wirklichkeit im Speicher eines Computers ist immer eine reduzierte Wirklichkeit. So wie eine Landkarte zwar verschiedene Aspekte einer Landschaft wiedergeben kann, aber nie die Landschaft als Ganzes, so kann ein Computermodell nur eine Auswahl wichtiger Faktoren erfassen, und diese Auswahl muß der Programmierer treffen. Deshalb sollte man die Aussagekraft von Simulationen nicht überschätzen. Sie geben wie Landkarten einen Überblick, aber als Propheten taugen sie nicht. So wird ein Computer, der die Funktionen eines Kernreaktors simuliert, zwar zeigen können, auf welche Weise Störfälle möglich sind, nicht aber, daß sie umöglich sind!
Auch viele für den CPC erhältliche Spiele stellen im Prinzip Simulationen dar, Sportspiele oder das Weltraumabenteuer Elite wären als Beispiel zu nennen. Doch während es hierbei im wesentlichen auf die Qualität der Grafik- und Soundeffekte ankommt, werden an wissenschaftliche Simulationsprogramme ganz andere Anforderungen gestellt. Sie sollen mit möglichst großer Exaktheit die Wirklichkeit quantitativ, d.h. in Form von Zahlenwerten wiederspiegeln. Dieses Material stellt für den Forscher eine geeignete Basis dar, um neue Erkenntnisse zu gewinnen oder bestimmte Theorien zu überprüfen. Auf den Uneingeweihten wirken lange Zahlenkolonnen oder verschlungene Bildschirmdiagramme jedoch im allgemeinen nicht besonders aufschlußreich.
Um mit solchen Programmen arbeiten zu können, sind schon recht solide mathematische Grundlagen erforderlich (z.B. Wachstumsfunktionen), deren Erörterung den Rahmen dieses Buches beiweitem sprengen würde. Deshalb werden wir als Einführung in den Themenbereich Ökologie-Simulation ein System behandeln, das zwar keinen Anspruch auf wissenschaftliche Exaktheit stellt, aber trotzdem eine ganze Reihe interessanter Experimente ermöglicht, und dabei auch etwas für's Auge bietet: Die Zeitraffer-Darstellung eines künstlichen kleinen Lebensraumes, in dem das Schicksal der Individuen nicht nur statistische Bedeutung hat, sondern auch einzeln beobachtet werden kann.
Ausgangspunkt ist also das im letzten Kapitel besprochene Game of Life, wobei jedoch einige wesentliche Änderungen vorgenommen werden. Zunächst soll jede Zelle des Spielfeldes nicht nur zwei, sondern vier verschiedene Zustände annehmen können. Um die Angelegenheit anschaulich zu gestalten, werden wir den Zuständen, repräsentiert durch die Zahlen von 0..3, sofort eine konkrete Bedeutung geben:
| 0 = leer |
| 1 = Gras |
| 2 = Schaf |
| 3 = Wolf |
Was nun während des Spielablaufs mit dem Inhalt einer Zelle passiert, hängt ähnlich wie beim Game of Life von der unmittelbaren Nachbarschaft ab; als Nachbarn sollen die vier direkt angrenzenden Zellen (oben, unten, links und rechts) gelten. Was mit einem Schaf passiert, das sich in der Nähe eines hungrigen Wolfes befindet, können Sie sich wahrscheinlich schon denken - doch zur exakten Formulierung der Spielregeln kommen wir gleich.

Zunächst ein weiterer wichtiger Unterschied zum Game of Life: Wie bereits erwähnt, ist das Modell von Conway streng deterministisch aufgebaut, es gibt dem Zufall keinen Raum. Über ein echtes ökologisches System kann man jedoch nur statistische Aussagen machen, also zum Beispiel über die Häufigkeit oder Wahrscheinlichkeit bestimmter Ereignisse. Wann und wo ein Wolf über ein Schaf herfallen wird, läßt sich nicht genau berechnen, die exakten Koordinaten der Ereignisse in Zeit und Raum sind vollkommen unbestimmt.
Dieser Tatsache soll in unserem Ökologie-Experiment Rechnung getragen werden, indem die Ereignisse laut Regelkatalog nicht mehr simultan auf dem gesamten Spielfeld ausgeführt werden, sondern nacheinander, wobei der Rechner jedes Mal den Ort des Geschehens mit Hilfe der RND-Funktion auswürfelt. Daß sich ein Schaf in der Nähe eines Wolfes nicht unbedingt sicher fühlen kann, ist damit weiterhin klar; nur wann es gefressen wird, das steht in den Sternen.
Hier nun die Gesetze, die die Nachbarschaftsbeziehungen in unserem WSG-Modell regeln:
In den Regeln (2) und (3) sind also Fressen und Vermehrung miteinander gekoppelt, was nicht unbedingt realistisch ist, aber zu sehr dynamischen Abläufen führt. Die Regeln (4) und (5) liefern Wölfe und Schafe dem Hungertot aus, wenn sie zu gierig werden.
Der CPC kann natürlich mit der sprachlichen Formulierung der Gesetze nicht viel anfangen, womit die Frage nach einer computergerechten Darstellung des Regelkatalogs auftaucht. Die Programmierung einer Fallunterscheidung mit Hilfe vieler IF..THEN-Statements ist zwar naheliegend, wird aber schnell unübersichtlich. Auch eine nachträgliche Änderung des Katalogs ist auf diese Weise nur sehr umständlich durchzuführen.
Für unsere Zwecke ist die im folgenden dargestellte Tabellenform wesentlich besser geeignet. Dieses System ist jedenfalls einfacher zu handhaben, als es auf den ersten Blick scheint: Die acht Spalten auf der rechten Seite und die mit Fragezeichen markierten Zeilen brauchen uns zunächst nicht interessieren, da sie nur für ein erweitertes System mit fünf Zellenzuständen eine Rolle spielen; und die Bedeutung der restlichen Eintragungen ist schnell geklärt.
| Nachbarschaft 0 = nicht vorhanden 1 = vorhanden |
Gras | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | |||
| Schaf | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | ||||
| Wolf | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | ||||
| ???? | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | ||||
| Umwandlungs- anweisungen für die mittlere Zelle |
0 = Leer | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |||
| 1 = Gras | 1 | 1 | 2 | 2 | 1 | 1 | 2 | 2 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ||||
| 2 = Schaf | 0 | 2 | 0 | 2 | 3 | 3 | 3 | 3 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ||||
| 3 = Wolf | 0 | 0 | 3 | 3 | 0 | 0 | 3 | 3 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ||||
| 4 = ??? | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
Der obere Teil der Tabelle stellt alle möglichen Nachbarschaftskonstellationen dar. Wer sich etwas mit Maschinensprache auskennt, hat sicherlich auf den ersten Blick festgestellt, daß hier die Binärzahlen von 0...15 versammelt sind, und zwar senkrecht geschrieben. Diese Anordnung hilft dem Rechner, nach der Analyse der Nachbarschaft die zuständige Spalte im Regelkatalog zu finden. Der untere Teil der Tabelle enthält die Umwandlungsanweisungen für die ausgewürfelte Zelle. Wenn der Rechner zum Beispiel ein Schaf erwischt, das von Gras und Wolf umgeben ist, so muß er in der sechsten Spalte von links nachschauen. In der für Schafe zuständigen Zeile 2 in der unteren Tabellenhälfte findet er dann am Kreuzungspunkt eine 3, das arme Schaf wird also durch einen neuen Wolf ersetzt.
Sie können sich anhand weiterer Beispiele davon überzeugen, daß die Tabelleneintragungen exakt die sechs Regeln für das WSGModell wiedegeben, wenn auch in recht abstrakter Form. Doch mit etwas Übung stellt die Codierung selbsterdachter Gesetze kein Problem dar. Für ambitionierte Programmierer wäre es vielleicht eine interessante Aufgabe, eine symbolische Öko-Sprache zu erfinden und eine Art Compiler zu schreiben, der daraus die Tabellenform erzeugt.
Das Simulationsprogramm OEKOEXP.BAS ist weitgehend modular aufgebaut und mit zahlreichen Kommentaren versehen, um auf einfache Weise Änderungen zu ermöglichen. Das Hauptprogram zu Beginn hat nur die Aufgabe, die verschiedenen Programmteile in der richtigen Reihenfolge aufzurufen.
Im Initialisierungsteil ab Zeile 1000 werden die Arrays für das Spielfeld, den Regelkatalog usw. dimensioniert. Die eigenliche Definition des WSG-Modells erfolgt ab Zeile 2000. Für die Darstellung der verschiedenen Bewohner unseres Öko-Systems werden Grafikzeichen mit doppelter Höhe erzeugt, die ab Zeile 2150 mittels einiger Steuerzeichen zusammengesetzt werden - sogar die dazugehörige Farbe wird mit CHR$(15) gleich integriert. Damit es bei der Ausgabe dieser Superzeichen am rechten Bildschimrand keine Probleme gibt, täuscht ein POKE im Initialisierungsteil dem CPC die Existenz von 40 Spalten in MODE 0 vor.
Auch die Regeltabelle wird in diesem Programmteil eingelesen; sie befindet sich in den DATA-Zeilen 2300 - 2340. Hier können Sie beliebige Änderungen vornehmen, um den Ablauf der Ökologie-Experimente zu beeinflussen. Das Unterprogramm ab Zeile 3000 bereitet den Spielablauf vor, indem es eine Zufallsverteilung von Wölfen, Schafen und Gras als Ausgangssituation erzeugt. Da es bei der der Erforschung der Nachbarschaft passieren kann, daß das Programm über den Rand hinausschaut, wird dem Spielfeld intern noch ein Rahmen verpaßt, der mit der neutralen Ziffer 9 belegt ist.
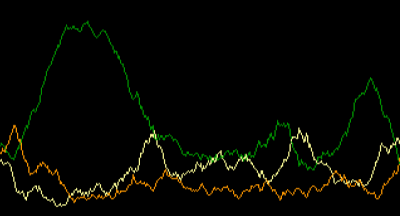
Der eigenliche Spielablauf findet ab Zeile 4000 statt. Zunächst wird auf einen Tastendruck als Startsignal gewartet, und danach ein Zeitintervall von vier Sekunden (200 * 1/50 sec) für die regelmäßige Bestandsaufnahme festgelegt, die vom Unterprogramm in Zeile 6000 vorgenommen wird: Es merkt sich die jeweiligen Populationszahlen, so daß sie das Modul in Zeile 5000 zum Abschluß als Funktion der Zeit grafisch darstellen kann.
Das Unterprogram ab Zeile 10000 steht den anderen Modulen zur Verfügung. Es führt nicht nur die Änderung der Zellinhalte aus, sondern bringt dabei auch die verschiedenen Zähler auf den neuesten Stand. Als Parameter werden die Koordinaten (X,Y) einer Zelle und der neue Inhalt in der Variablen neu Übergeben.
Nach dem Programmstart, der Erzeugung der Anfangsverteilung und dem Beginn des Spielablaufs wird sich ein recht munteres Treiben auf dem Bildschirm entfalten; zusätzlich geben noch drei Zähler im unteren Bildschirmbereich über die aktuellen Populationszahlen Auskunft. Ein weiterer Zähler zeigt laufend die Anzahl der ausgewürfelten Ereignisse an. Wie sich schon nach wenigen Versuchen herausstellt, ergeben sich vollkommen andersartige Abläufe als beim Game of Life. Während das im letzten Kapitel beschriebene Simulationsspiel eine Neigung entwickelte, nach einiger Zeit in festen Formen zu stagnieren, führt die zufallsgesteuerte Dynamik des WSG-Modells leicht zu Katastrophen, bei denen eine oder mehrere Arten vollkommen aussterben.
Zwar sind die WSG-Gesetze so formuliert, daß sie extremen Entwicklungen entgegenwirken: Eine starke Vermehrung der Schafe zieht zum Beispiel auch eine entsprechende Vermehrung der Wölfe und Reduzierung der Nahrung nach sich. Da aber die räumliche Verteilung der Lebewesen in unserem Spiel eine starke Rolle spielt, setzen die Regelmechanismen oft erst verzögert ein, und es entstehen mehr oder minder starke Schwankungen der Populationszahlen, was sich nach dem Abbruch mit <ENTER> sehr schön aus den gezeichneten Kurven ersehen läßt. Insbesondere bei einem beschränkten Spielfeld von nur 200 Zellen kommt es dabei leicht zu Fluktuationskatastrophen. Wie stark in der Tat die Elastizität eines ökologischen Systems von der Größe des Lebensraumes abhängt, soll nun ein weiteres Experiment zeigen.
Zu diesem Zweck muß mit Hilfe der MERGE-Anweisung die Erweiterung 1 (OEKOERW1) in das Hauptprogramm integriert werden. Sorgen Sie dafür, daß sich das Hauptprogramm im Speicher befindet, und geben Sie dann MERGE "OEKOERW1" ein, worauf die neuen Programmteile dazugeladen werden. Auch die noch folgenden Ergänzungen Lassen sich auf diese Weise einbauen. vorher muß jedoch immer das Originalprogramm OEKOEXP.BAS neu geladen werden, da sich die Erweiterungen untereinander nicht vertragen!
Die Erweiterung 1 zerlegt das Spielfeld durch eine Autobahn in zwei voneinander isolierte Teile. Dazu tritt noch eine neue Regel in Kraft:
(7) Schafe und Wölfe in der Nachbarschaft der Autobahn werden überfahren, also durch ein Leerfeld ersetzt.
Für die Darstellung der Autobahn wird intern die Ziffer 4 als fünfter Zellenzustand benutzt, ein Beispiel dafür, daß sich mit dieser Codierung nicht nur Lebewesen darstellen lassen. Der neue Regelkatalog für das erweiterte System enthält in der letzten Zeile natürlich nur Vieren, da die Autobahn nicht umgewandelt werden kann.
Die linken acht Spalten entsprechen den ursprünglichen WSG-Gesetzen, die rechten acht Spalten spiegeln die Änderungen wieder, die sich in direkter Nahe der Autobahn ergeben. Wie ein paar Versuche zeigen, ist zumindest in einem der beiden Teilbereiche meist schon nach kurzer Zeit das ökologische Gleichgewicht zerstört. Die unmittelbare Wirkung der Autobahn spielt dabei noch nicht einmal die entscheidende Rolle. Viel schlimmer wirkt sich die herabgesetzte Toleranzbreite für die natürlichen Schwankungen des System aus. Ein kleines System ist mit einer Differenz von +/- 20 Tieren natürlich viel eher überfordert als ein großer Lebensraum - ein statistischer Effekt, der bei der Landschaftsplanung leicht übersehen wird.
Auf der anderen Seite stellt sich natürlich die Frage, welche Maßnahmen geeignet sind, um solche Katastrophen zu verhindern. Zwei Ansätze sollen im Folgenden untersucht werden:
Unser WSG-Modell ist ein sogenanntes dissipatives System, das zu einer Aufrechterhaltung ständig Energie umsetzt. Diese Energie wird durch das nachwachsende Gras repräsentiert; ohne Graswuchs haben sowohl Schafe als auch Wölfe keine Überlebenschance. Eine Verbesserung der Energieversorgung läßt sich sehr einfach erreichen, indem man in die erste DATA-Zeile des Regelkatalogs durchweg Einsen schreibt, wonach die Regel (1) folgende Gestalt annimmt:
(1) Ein Leerfeld wird auf jeden Fall mit neuern Gras belegt.
Damit kann das Gras also an jeder beliebigen Stelle neu wachsen (z.B. durch Samenflug), die Nachbarschaft anderer Pflanzen ist nicht mehr notwendig. Einige Tests zeigen schnell, daß auf diese Weise in der Tat mehr Stabilität gegeben ist; das Spiel läuft im Schnitt wesentlich länger katastrophenfrei. Allerdings sind solche idealen Verhältnisse nur bedingt realistisch: Ein derart ungehemmtes Pflanzenwachstum wird im allgemeinen nur zeitweise, also im Frühling oder Sommer stattfinden.
Eine kritische Situation tritt bei dem WSG-Modell oft schon kurz nach Beginn auf. Die gute Durchmischung der Lebewesen in der Startverteilung führt zu einem starken Anwachsen der Wolfspopulation und einer Reduzierung der Vegetation, wodurch prompt die Schafe in eine Krise kommen. Doch Hilfe naht: Wir werden mit der Erweiterung 2 ein paar Jäger ins Feld schicken, um den Bestand an Wölfen knapp zu halten. Gehen Sie zu diesem Zweck genau wie bei der ersten Erweiterung vor: Laden Sie das Hauptprogramm OEKOEXP.BAS neu und geben Sie dann MERGE "OEKOERW2" ein. Durch neue DATA-Zeilen für den Regelkatalog werden folgende Gesetze eingeführt:
Die Folgen dieser Ergänzung sind jedoch sehr drastisch: In den meisten Fällen werden die fleißigen Jäger recht schnell ein Aussterben der Wölfe bewirken, was zwar den Schafen im ersten Momment gut tut, aber nicht dem Gras. Der Bildschirm wird regelrecht kahlgefressen. Nur die daraufhin einsetzende Hungerkatastrophe verhindert mitunter eine totale Einöde.
Wie Sie sehen, ist es also gar nicht so einfach, ein System zu gestalten, daß sich dynamisch und trotzdem stabil verhält. Wer den Ehrgeiz entwickelt, durch Herumbasteln am Regelkatalog seine Idealökologie zu entwickeln, sollte dabei beachten, daß sich die Tendenz eines System im allgemeinen erst nach mehreren Durchläufen erkennen läßt. Durch den starken Einfluß des Zufalls zeigt ein einzelner Spielablauf immer nur, was passieren kann, aber nicht, was passieren wird! Aus diesem Grund ist unser Programm zwar recht spannend, aber in der vorliegenden Form nicht geeignet, um wissenschaftliche Theorien zu entwickeln: Es fehlt die Reproduzierbarkeit der Versuchsergebnisse.
Andererseits bietet unser Öko-Experiment jedoch einen Ansatz, der bei wissenschaftlichen Programmen meist nicht gegeben ist: Es läßt sich zu einem recht interessanten Spielprogramm ausbauen. Bislang bestand zwar nur die Möglichkeit, die Regeln zu definieren und sich den Ablauf passiv anzuschauen, doch eine dritte Erweiterung soll zeigen, wie eine direkte Eingriffsmöglichkeit programmiert werden kann.
Der Programmteil OEKOERW3, der genau wie die vorherigen Ergänzungen mit MERGE eingebunden wird, bringt einen Jäger auf das Spielfeld, den Sie mit Hilfe der Cursortasten herumwandern lassen können. Bereits mit Wölfen oder Schafen besetzte Zellen kann er natürlich nicht betreten, und da er weiterhin das Gras unter seinen Füßen zertrampelt, sollten Sie ihn etwas behutsam durch die Landschaft bewegen.
Auf der anderen Seite stehen ihm jedoch auch einige Aktionsmöglichkeiten zur Verfügung. Wenn Sie die <SPACE>-Taste gedrückt halten und zusätzlich die Cursortasten betätigen, wird je nach Lage der Dinge in der entsprechenden Richtung ein Leerfeld mit Gras bepflanzt oder auch ein Wolf oder Schaf abgeschossen. Doch nichts ist ohne Risiko: Wie Sie der letzten DATA-Zeile entnehmen können, ist der Jäger auch als Futter für die Wölfe vorgesehen. Wenn er sich in der Nachbarschaft eines Wolfes befindet und in diesem Moment zufällig ausgewürfelt wird, ist es um ihn geschehen!
Auf diese Weise können Sie also regulierend in den Ablauf Ihrer Ökologie-Experimente eingreifen. Für einen echten Spiele-Hit fehlt dem Programm zwar noch eine spannungsvolle Motivation, doch das läßt sich mit einigen zusätzlichen Ideen ändern. Hier ein paar Anregungen:
Benutzen Sie mehrere Regelkataloge, die periodisch oder zufallsgesteuert ausgetauscht werden, um Jahreszeiten oder Seuchen zu simulieren.
Der letzte Punkt ist allerdings programmtechnisch nicht leicht in den Griff zu bekommen, da die Menge M der Eintragungen in der Regeltabelle mit der Anzahl Z der möglichen Zellenzustände nach der Formel
M = Z * 2(z-1)
exponentiell anwächst. Hier müßte man also eventuell noch einen geeigneteren Algorithmus finden.
Ergänzende Literatur: