Leistungsfähige, grafisch orientierte Computersysteme gewinnen in der Industrie, Wissenschaft und Kunst zunehmend an Bedeutung. Die Entwicklung und Darstellung hochkomplexer Strukturen ist in vielen Fällen überhaupt erst durch den Einsatz bildverarbeitende Systeme möglich geworden. Und erstaunlich genug - oft liefern selbst rein zweckorientierte Forschungsprojekte ein Bildmaterial, das man eher einem genialen Künstler zutrauen möchte. Die im letzten Kapitel behandelten Chaos-Grafiken stellen sicherlich eines der erstaunlichsten Beispiele in dieser Hinsicht dar.
Doch bei aller Begeisterung für die Möglichkeiten der neuen Technologie sollte man nicht vergessen, daß sich in der Natur zahlreiche Kreationen finden lassen, neben denen die meisten Computergrafiken recht blaß aussehen. Haben Sie schon einmal Schneekristalle durch die Lupe oder ein Mikroskop betrachtet? Falls nicht, so sollten Sie es bei nächster Gelegenheit nachholen, oder zumindest lesen, was der Schriftsteller Thomas Mann über dieses Erlebnis berichtet:
Kleinodien, Ordenssterne, Brillantgaraffen, wie der getreueste Juwelier sie nicht reicher und minuziöser hätte herstellen können... und unter den Myriaden von Zaubersternchen in ihrer untersichtigen, dem Menschenauge nicht zugedachten, heimlichen Kleinpracht war nicht eines dem anderen gleich.
Der unerschöpfliche Erfindungsgeist, mit dem die Natur milliardenfache Variationen des Themas sechsstrahlige Symmetrie erzeugt, erscheint nach wie vor als ein unbegreifliches Wunder. Und doch ist es inzwischen mit Hilfe intelligent ausgedachter Computersimulationen gelungen, zumindest einige der Grundprinzipien dieser Naturvorgänge zu erforschen und zu verstehen.
So konnte unter anderem gezeigt werden, daß ein einfacher Satz geeigneter Regeln (Naturgesetze), wiederholt angewendet auf bestimmte Grundelemente (Moleküle), mit fast zwingender Notwendigkeit Strukturen beliebiger Komplexität erzeugt. Aufgrund dieser Erkenntnisse sprechen manche Forscher von einer Selbstorganisationsfähigkeit der Materie, eine Theorie, die zu weitreichenden Kosequenzen führt. Wie ist zum Beispiel das Leben auf unserem Planeten entstanden - ein einmaliger Zufall? Wenn die Materie unter der Einwirkung der Naturgesetze die Fähigkeit erlangt, sich selbst zu strukturieren, so ist vielleicht die individuelle Ausprägung der Lebensformen zufallsbedingt, nicht aber die Tatsache des organischen Lebens an sich. Es mußte mit hoher Wahrscheinlichkeit entstehen, sobald die entsprechenden Rahmenbedingungen gegeben waren!
Wie aus einfachsten Voraussetzungen außerordentlich komplexe Muster entstehen können, soll nun ein kleines SoftwareExperiment auf dem CPC demonstrieren, ein wahres Kabinettstück der mathematischen Experimentalkunst. Eine derart kunstvolle Filigrangrafik, wie sie das Programm Reproduktionsmuster (REPRO.BAS) erzeugt, haben Sie wahrscheinlich auf Ihrem Bildschim noch nicht gesehen! Das Programm operiert mit den denkbar einfachsten Grundelementen, nämlich mit Bildpunkten, die entweder gesetzt (hell) oder zurückgesetzt (dunkel) sind. Dazu kommen noch zwei Gesetze, die iterativ (wiederholt) auf dem gesamten Bildschirm angewendet werden:
Alle Punkte, die auf diese Weise bei einem Durchgang neu entstehen, werden als eine Generation bezeichnet. Mit dieser Definition kann die zweite Regel formuliert werden:
Die Punkte gehen also nach einiger Zeit an Altersschwäche zugrunde; nach jedem Durchgang sind exakt die jeweils letzten zwei Generationen auf dem Bildschirm zu sehen. Solange die Regeln auf einen leeren Bildschirm angewendet werden, passiert natürlich überhaupt nichts. Doch ein einziger Punkt, der in Zeile 410 des Programms als Kristallisationskeim gesetzt wird, bringt die Lawine ins Rollen. Das folgende Bild verdeutlicht das Prinzip und zeigt die Entwicklung der ersten fünf Generationen:
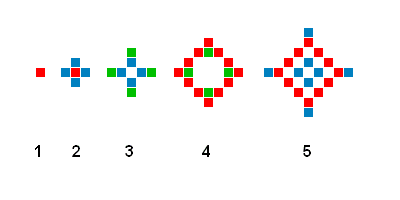
Das durch CALL &A000 aufgerufene Maschinenprogramm führt die Regeln aus und sorgt für die Bildschirmdarstellung. Übrigens wurden bei der Programnierung spezielle Techniken zur Erzeugung schneller Grafik benutzt, die direkt mit dem Bildschirmpeicher operieren. Die normalen Systemroutinen oder ein Basicprogranm wären hoffnungslos zu langsam, da pro Generation bis zu 384000 Punkte auf ihre Farbe getestet werden müssen!
Die Darstellung der Generationen durch verschiedene Farben hat nicht nur ästhetische Gründe. Sie ermöglicht es dem Programm, die Generation (n-2) zu erkennen, ohne eine Unmenge Koordinaten abzuspeichern. Weiterhin erlaubt die Farbdarstellung die quasi-synchrone Anwendung der Gesetze: Die während der Erzeugung der aktuellen Generation bereits gesetzten Punkte werden noch nicht als Nachbarn gezählt. Natürlich kann der Computer nicht wie gefordert alle Bildpunkte gleichzeitig erfassen, sondern nur nacheinander behandeln - eine Tatsache, die durch geeignete Programmiertricks ausgeglichen werden muß, um Störungen zu vermeiden.
Wer noch gerne etwas mit diesem System experimentieren möchte, kann eine veränderte Anfangssituation ausprobieren. Der in Zeile 410 erzeugt Punkt kann z.B. durch einen Buchstaben oder ein Grafiksymbol ersetzt werden. Sehr reizvoll sind auch Bilder, die aus mehreren auf dem Bildschirm verteilten Keimen entstehen. 0bwohl die typische Charakteristik der erzeugten Grafiken erhalten bleibt, ergibt sich je nach Startfigur ein anderer Ablauf, und die Analogie zur Enstehung von Schneekristallen wird deutlich: Die Ausprägung der Form bestimmt der Kristallkeim (z.B. ein Staubkorn), die charakteristische Symmetrie entsteht jedoch durch die Gesetzmäßigkeiten der molekularen Bindungskräfte.
Bevor wir uns einem weiteren, auf ähnlichen Grundlagen beruhenden Software-Experiment zuwenden, soll zunächst daran erinnert werden, auf welche Weise der CPC Informationen verarbeitet. Wie Sie sicherlich wissen, enthält Ihr Computer einen Mikroprozessor als zentrale Steuerungseinheit. Er liest binäre Werte aus den Speicherzellen, verknüpft sie in seinen internen Registern nach bestimmten Regeln, und legt das Ergebnis wieder in anderen Speicherzellen ab.
Diese Art der Informationsverarbeitung nennt man sequentiell: Komplizierte Berechnungen werden ausgeführt, indem die dazu notwendigen Schritte nacheinander programmgesteuert abgearbeitet werden. Nach diesem Prinzip funktionieren praktisch alle Digitalcomputer, und nur die hohe Verarbeitungsgeschwindigkeit erzeugt mitunter den Eindruck, der Rechner könne mehrere Dinge gleichzeitig erledigen.
Der Computer ist damit ein getreues Abbild des sprachorientierten menschlichen Verstandes. Auch die verbale Informationsverarbeitung kann nur sequentiell erfolgen. Versuchen Sie einmal, bewußt zwei verschiedene Gedanken gleichzeitig zu denken: Sie werden sehen, es ist praktisch unmöglich.
Allerdings stellt der Verstand auch nur einen sehr kleinen Ausschnitt des informatischen Systems Mensch dar. Schon die verschiedenen Formen der Sinneswahrnehmung erfordern ein Verarbeitungssystem, das nach einem ganz anderen Prinzip arbeitet. Es ist ja ohne weiteres möglich, mehrere Dinge gleichzeitig zu sehen oder zu fühlen - mit anderen Worten, der Mensch kann eine große Anzahl verschiedener Daten parallel erfassen.
Der Verstand ist zwar in der Lage, die von den Sinnesorganen gelieferten Informationen auf einer abstrakten Ebene zu analysieren, doch für die unmittelbare Auswertung ist er effektiv zu langsam. Stellen Sie sich einmal vor, Sie müßten, um ein Haus zu erkennen, das Bild bewußt in ein Punktraster zerlegen, jedem Punkt einen Farb- und einen Helligkeitswert zuordnen, die Daten dann mit einem bereits gespeicherten Raster vergleichen und daraus einen Wert ermitteln, der Ihnen verrät, mit welcher Wahrscheinlichkeit es sich um ein Haus handelt... des langen Satzes kurzer Sinn: Sie wären praktisch handlungsunfähig!
Dieses Beispiel macht deutlich, warum selbst die besten und schnellsten Computer trotz aller Bemühungen der Forscher nicht in der Lage sind, im menschlichen Sinne zu sehen oder zu hören: Ihr Arbeitsprinzip ist dazu einfach ungeeignet. Zwar werden inzwischen schon Versuche mit Multiprozessor-Systemen unternommen, doch auch hierbei ergeben sich erhebliche praktische Schwierigkeiten. So kam man z.B. nicht erwarten, daß ein Rechner mit 100 Prozessoren 100 mal so schnell wie ein normaler Computer läuft, da ein Teil der Kapazität gebraucht wird, um den Datentransfer zwischen den verschiedenen Einheiten zu koordinieren.
Interessanterweise existiert jedoch ein Ansatz zur Lösung dieser Probleme der bereits in der Vorcomputerzeit von dem Mathematiker John v. Neumann theoretisch untersucht wurde. Die schon 1936 von Alan M. Turing aufgeworfenen Frage nach der möglichen Existenz einer universellen Denkmaschine veranlaßte ihn zur gedanklichen Konstruktion eines sogenannten Zellautomaten. Dabei handelt es sich um einen homogenen, zellulär unterteilten Raum, in dem jede Zelle eine bestimmte Anzahl von Zuständen annehmen kann (z.B. verschiedene Farben). Auf alle Zellen wird synchron ein Satz von Umwandlungsregeln (Transition Rules) angewendet, deren Ausführung im einzelnen vom Zustand der jeweiligen Zelle und der angrenzenden Nachbarzellen abhängt.
John v. Neumann konnte theoretisch nachweisen, daß eine Konfiguration aus 200.000 Zellen mit jeweils vier Nachbarn und 29 Zustandsmöglichkeiten ausreicht, um im Prinzip jede denkbare Rechenoperation auszuführen. Solch ein Zellautomat enthält keinen zentralen Prozessor, sondern die Speicherzellen komunizieren ohne Umschweife direkt miteinander. Mit jedem Taktimpuls, der im gesamten Raum Umwandlungen laut Regelkatalog bewirkt, werden eine große Anzahl von Operationen gleichzeitig ausgeführt. Informationen erscheinen dabei nicht mehr als Bits und Bytes, sondern als Raum- oder Flächenmuster, die sich überlagern und gegenseitig beeinflussen können - ein Prinzip, das die Natur auch bei der Konstruktion des menschlichen Gehirns angewendet hat.
Die wohl bekannteste Veranschaulichung des Zellautomaten-Prinzips ist das 1970 vom britischen Mathematiker Conway erfundene Game of Life. Wie in unserem vorherigen Experiment kann in diesem Spiel jede Zelle zwei verschiedene Zustände annehmen; sie ist also entweder bewohnt oder unbewohnt. Allerdings wurde die Nachbarschaft auch auf die diagonal angrenzenden Zellen erweitert - jede Zelle hat also acht Nachbarzellen - und die Umwandlungsregeln wurden so formuliert" daß die Abläufe recht realistisch die Folgen von Isolation, überbevölkerung oder Kooperation in einer Gesellschaft lebendiger Wesen darstellen.
Die Regeln lassen sich durch zwei einfache Kommandos erfassen:
Eine weitere Darstellungsmöglichkeit für diese Gesetze ist ein computergerecht gestalteter Regelkatalog in Tabellenform. Es gibt die Belegung einer Zelle in der Generation (n+1) in Abhängigkeit von ihrem momentanen Zustand und der Anzahl der Nachbarn an. Eine 1 bedeutet, daß die Zelle in der nächsten Generation bewohnt sein wird, eine 0 steht dagegen für eine leere Zelle:
| Anzahl der Nachbarn | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|---|
| 0 - Zelle wird zu | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 |
| 1 - Zelle wird zu | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 |
Auf den ersten Blick scheinen die Lebensbedingungen der Life-Einzeller also ziemlich schlecht zu sein, sie reagieren sehr enpfindlich auf Einsamkeit oder Überbevölkerung. Einige Versuche zeigen jedoch recht schnell, daß gerade diese Einschränkungen dem System seine Dynamik verleihen und zu hochinteressanten Abläufen führen. Nicht umsonst hat dieses Spiel nach seiner Entstehung an Universitäten und wissenschaftlichen Instituten für allerhand Aufsehen und mitunter sogar Ärger gesorgt, da die Terminals der Rechenanlagen regelmäßig von Life-Fanatikern blockiert wurden - für jedermann verfügbare Heimcomputer gab es ja in den siebziger Jahren noch nicht.
Doch die Zeiten haben sich glücklicherweise geändert, und Sie können mit Hilfe des Programms Game of Life (LIFE.BAS) stundenlang auf Ihrem CPC experimentieren, ohne befürchten zu müssen, daß Sie im nächsten Augenblick das Betriebssystem wegen Überschreitung der Rechenzeit aus dem Rechner wirft.
In dem Program werden die Zellen nicht wie bei den Reproduktionsmustern pixelweise, sondern etwas vergrößert dargestellt; insgesamt steht eine Fläche mit 50x80 = 4000 Zellen zur Verfügung. Die Umwandlungsregeln führt wieder ein kleines Maschinenprogramm aus, es schafft etwa zwei Generationen pro Sekunde. Besonderen Wert wurde auf eine extrem schnelle Bildschirmausgabe gelegt. In der Tat scheinen die Umwandlungen auf der gesamten Fläche gleichzeitig zu erfolgen.
Nach dem Programmstart erscheint zunächst das leere Spielfeld, das mit einem Karomuster vorstrukturiert ist, um eine genaue Analyse der einzelnen Abläufe zu ermöglichen. Um sich einen Eindruck von dem Treiben der Life-Einzeller zu verschaffen, können Sie zunächst die Taste <Z> drücken, worauf der Rechner eine Zufallsverteilung auf dem Bildschirm produziert. Warten Sie eine Weile, bis die Fläche einigermaßen voll ist, und brechen Sie dann den Vorgang mit <ENTER> ab. Mit Hilfe der <SPACE>-Taste können Sie nun die jeweils nächste Generation erzeugen, oder auch mit <A> die Generationswechsel automatisch ablaufen lassen. Auch diese Funktion wird mit <ENTER> abgebrochen.
Um gezielt die Eigenschaften bestimmter Konfigurationen zu untersuchen, kam mit <E> ein kleiner Editor angewählt werden. Der Cursor wird wie üblich mit den Pfeiltasten gesteuert; die Taste <1> belegt die Zelle auf Cursorposition, die Taste <0> löscht sie entsprechend. Um ganze Reihen von Life-Wesen zu produzieren, können Sie auch die Taste <1> gedrückt halten und den Cursor über den Bildschirm wandern lassen, er hinterläßt dann eine Spur von gefüllten Zellen. Mit <ENTER> wird der Editmodus wieder verlassen; mit <L> bei Bedarf die gesamte Fläche gelöscht.
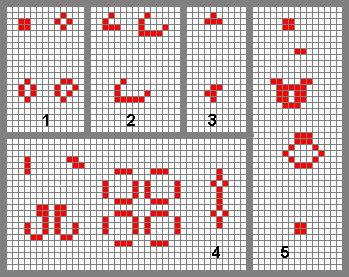
Das obige Bild zeigt einige typische Life-Konfigurationen. Die mit 1 bezifferte Gruppe enthält vier stabile Figuren, die bei den Generationswechseln unverändert bleiben. Gruppe 2 zeigt drei sogenannte Gleiter. Bei diesen Figuren handelt es sich um Oszillatoren, die periodisch ihre alte Form wiedererlangen, sich dabei aber um ein kleines Stück weiterbewegen. Stationäre Oszillatoren mit einer Periode von 2 bis 15 Generationen finden Sie dagegen in der Gruppe 4 versammelt. Ein besonders eigenartiges Verhalten zeigt der 30-Generationen-Oszillator, der die Gruppierung 5 bildet: Er produziert, ohne dabei an Substanz zu verlieren, eine Serie kleiner Gleiter, die nach rechts abwandern.
Die Gruppe 3 enthält noch zwei Figuren, die ein expansives Verhalten zeigen. Während die obere Figur jedoch schon nach wenigen Generationen in vier stationäre Oszillatoren zerfällt, ist die untere Figur ohne weiteres in der Lage, den gesamten Bildschirm mit ihren Nachkommen zu füllen. Sie gilt als die kleinste Figur, die sich beliebig weit ausdehnt; bisher konnte kein definierter Endzustand ermittelt werden.
Wenn Sie die abgebildeten Muster alle gemeinsam testen wollen, entfernen Sie am besten die expansive Figur und die drei Gleiter aus dem Sortiment, um die anderen Figuren nicht zu stören. Ansonsten ist es aber sehr interessant, was sich bei einer Kollision verschiedener Muster abspielt: sowohl eine totale Auslöschung als auch die Entstehung neuer Figuren kann die Folge sein. Durch die eifrigen Bemühungen der vielen Life-Forscher ist es inzwischen sogar gelungen, Muster zu finden, die durch gegenseitige Beeinflussung logische Funktionen wie etwa NOT, AND, OR oder XOR simulieren - ein wichtiger Schritt in Richtung eines praktisch anwendbaren Zellautomaten.
Ein Problem, das die Realisierung eines auch nur kleinen Zellrechners auf dem CPC verhindert, ist leider die unvermeidliche Spielfeldbegrenzung. Selbst eine 320x200-Fläche wäre noch viel zu klein. Das Programm betrachtet alle Zellen außerhalb der Fläche als leer, und daraus ergeben sich empfindliche Störungen, sobald ein Muster an den Rand stößt. Auf interessante Weise arrangiert sich allerdings der Gleiter oben rechts mit dieser Beschränkung: Er wird reflektiert und verwandelt sich dabei in einen kleineren Gleiter!
Wie man bei eigenen Experimenten feststellen kann, führt die Begrenzung des Lebensraumes dazu, daß alle Konfigurationen nach einiger Zeit steckenbleiben; es bleiben nur noch stabile Muster und Oszillatoren übrig, die keine grundsätzlich neuen Entwick lungen mehr bewirken können. Doch dieses Phänomen hat noch eine andere Ursache: Im Game of Life ist der schöpferische Zufall nicht vorgesehen. Der gesamte Prozeß läuft deterministisch ab, d.h. mit einer gegebenen Anfangssituation steht praktisch schon in allen Einzelheiten fest, was passieren wird. Sie können aber einmal erforschen, was die folgenden zusätzlichen Programmzeilen bewirken:
981 f=l 982 re= INT (RND*50) + 1 983 sp= INT (RND*80) + 1 984 GOSUB 1060
Wenn Sie jetzt den automatischen Generationswechsel mit <A> anwählen, wird bei jedem Durchgang ein neues Wesen an einem zufälligen Ort geboren und bringt etwas Abwechslung in die Angelegenheit. Wie bereits im 1. Kapitel angedeutet, spielt der Zufall bei der Erzeugung dynamischer (lebendiger) Strukturen ja eine wichtige Rolle.
Und es gibt noch eine weitere sehr interessante Experimentiermöglichkeit: In den DATA-Zeilen 530 und 540 steht der vorhin bereits erwähnte Regelkatalog für das Game of Life. Hier können sie natürlich die Nullen und Einsen auch anders verteilen und damit neue Umwandlungsgesetze gestalten. Die Abläufe, die sich aus einem veranderten Regelkatalog ergeben, stellen ein recht unerforschtes Gebiet dar und bieten noch viel Raum für aufregende Entdeckungen.
Nach dieser schon recht eindrucksvollen Simulation eines Zellautomaten drängt sich die Frage auf: Wieso ist eigentlich eine solche Maschine noch nicht gebaut worden? An der Hardware dürfte es nicht scheitern, die nötigen Chips wären mit dem heutigen technischen Stand sicherlich realisierbar. Doch das Problem liegt ganz woanders: Kein Mensch weiß, wie man einen Zellautomaten programmieren könnte.
Wie bereits erörtert wurde, beruht jede Sprache - und damit auch jede Programmiersprache - auf einer sequentiellen Logik. Zwar können wir auch über Ereignisse sprechen, die simultan stattfinden, jedoch nur, indem wir sie nacheinander beschreiben. Deshalb ist es sehr zweifelhaft, ob ein leistungsfähiger Zellautomat, der hunderte und tausende von Operationen gleichzeitig durchführt und dabei unzählige sich kreuz und quer gegenseitig beeinflussende Muster bildet, jemals mit den Mitteln eines sequentiell arbeitenden Verstandes beherrscht werden kann.
Bisher ist nur ein einziger Ausweg aus diesem Dilemma sichtbar: Die Maschine muß sich selbst programmieren! Wenn Sie Ihren CPC programmieren, so formulieren Sie mit Hilfe einer Programmiersprache einen Algorithmus, der Schritt für Schritt angibt, wie aus einer Situation A das Resultat B erzeugt wird. Wie einfach wäre es doch, wenn Sie den Computer einschalten und zu ihm sprechen könnten: 'Hier mein elektronischer Freund, das ist ein Schachbrett, das sind die Figuren, und so gehen die Regeln... und du hast gewonnen, wenn du meinen König eroberst, bevor ich deinen erwische. Spiele so, daß du nach Möglichkeit gewinnst!'
Sehen Sie - genau das müßte der Zellautomat können: Selbständig Lösungswege finden. Wie bereits gezeigt wurde, stellt es kein Problem dar, sich selbst organisierende Systeme zu erschaffen. Mit ein paar Umwandlungsregeln, die irgendwelche Muster erzeugen, ist es in diesem Fall jedoch nicht getan. Um gut Schach zu spielen, müßte die Maschine zielgerecht problembezogene Strukturen produzieren, ungünstige Muster verwerfen, Erfahrungen sammeln und selektiv auswerten... mit anderen Worten, einen Lernvorgang, eine Evolution nachvollziehen.
Doch die Formulierung von Bewertungsschemata, die einen sich selbst organisierenden Prozeß zielgerichtet ablaufen lassen, ist bisher ein theoretisch nur ansatzweise gelöstes Problem. Hinweise liefert allerdings ein Forschungsbereich, der sich mit dem Grenzgebiet zwischen Biologie und Informatik beschäftigt. Welche Strategien hat die Natur bei der Entwicklung des Lebens angewendet? Welche statistischen Gesetzmäpigkeiten tragen dazu bei, daß sich bestimmte Arten entfalten, während andere aussterben?
Das nächste Kapitel des Software-Experiments wird noch weiteres Material zu diesem Thema liefern. Wer sich intensiver mit diesem Gebiet beschäftigen möchte, dem sei das Buch Das Spiel - Naturgesetze steuern den Zufall von Manfred Eigen/Ruthild Winkler (Piper Verlag) empfohlen. Es enthält zahlreiche Simulationsspiele, die sich auch auf einem Heimcomputer gut realisieren lassen.