Nicht nicht nur in der Arbeitswelt erzeugt die moderne Computertechnik revolutionäre Veränderungen. Auch Wissenschaftlern und Künstlern stehen in zunehmenden Maße Hilfsmittel zur Verfügung, deren Möglichkeiten sich heute noch gar nicht vollständig abschätzen lassen.
So ist es zum Beispiel mit dem Hochleistungs-Computer CRAY X-MP möglich geworden, die Enstehungsgeschichte unseres Universums zu rekonstruieren und auf einem Bildschirm grafisch darzustellen. Wer schon einmal mit der Differentialgleichung zu tun hatte, die die Bewegung nur eines Planeten um die Sonne beschreibt, kann ermessen, welchen Rechenaufwand die Wechselwirkungen zwischen einer wahrhaft astronomischen Anzahl von Himmelskörpern erfordern.
Der Wissenschaftler früherer Zeiten, der praktisch nür über den Rechenschieber und die Logarithmentafel als Werkzeug verfügte, wäre damit hoffnugslos überfordert gewesen. Erst durch die Mikroelektronik ist es möglich geworden, komplizierte mathematische oder physikalische Systeme durch Simulationen experimentell zu erforschen. Besonders bemerkenswert ist dabei, daß die Ergebnisse dieser Experimente nicht nur in abstrakter Form als Zahlen oder Gleichungen vorliegen, sondern teilweise faszinierende Bilder ergeben. Wie ein Fernrohr oder ein Mikroskop erlaubt der Computer Einblicke in Welten und Dimensionen, die dem menschlichen Auge sonst verschlossen blieben. Mathematisch--logische Strukturen werden sichtbar, erscheinen als Farben und Formen auf dem Bildschirm, können experimentell und spielerisch verändert werden - kein Wunder also, daß die lange Zeit als trocken verschrieene Mathematik enorm an Attraktivität gewonnen hat.
Nicht nur Künstler entdecken hier neue Motive und Ausdrucksmöglichkeiten; auch Jugendliche entwickeln zunehmend ein lebhaftes Interesse an dieser Wissenschaft, die erst durch das Medium Computer im wahrsten Sinne des Wortes anschaulich geworden ist. Als erstes Software-Experiment soll deshalb ein Programm vorgestellt werden, das mit einer relativ einfachen mathematischen Formel eine Vielzahl verblüffender Bilder erzeugt, die unter dem Namen Chaos-Grafiken oder Apfelmännchen bereits für einiges Aufsehen gesorgt haben.
Die Apfelmännchen-Grafiken entstehen durch die bildliche Darstellung der Eigenschaften komplexer Zahlenfolgen - was sind überhaupt komplexe Zahlen? Wie ist es möglich, daß eine mathematische Formel Strukturen erzeugt, die durch die ihre geordnete Unregelmäßigkeit fast schon organischen Charakter haben? Um der Anwort auf diese Frage näher zu kommen, beginnen wir mit einem kleinen Ausflug in die Arithmetik, die Theorie der Zahlen:
Am Anfang der Entwicklung des Zahlbegriffs standen die natürlichen Zahlen 1, 2, 3, .... natürlich wohl deshalb, da sie nicht aus theoretischen Uberlegungen entstanden, sondern direkt aus der Anschauung. Der Urmensch trat aus seiner Höhle und begann zu zählen: 1 Säbelzahntiger, 2 Säbelzahntiger... - nun, wenn auch vielleicht nicht genau so, aber so ähnlich müssen die natürlichen Zahlen entstanden sein. Und für viele Zwecke reichen sie wirklich aus! Wir können sie addieren oder multiplizieren, und das Ergebnis wird wieder eine natürliche Zahl sein. Der Bereich der natürlichen Zahlen ist also hinsichtlich dieser Operationen abgeschlossen, wie der Mathematiker sagt.
Probleme tauchen jedoch auf, wenn wir subtrahieren oder dividieren wollen. Manchmal geht es gut, aber manchmal auch nicht, wie die Gleichung x+ 5 = 3 zeigt; sie hat im Bereich der natürlichen Zahlen keine Lösung. Um diesen unbefriedigenden Zustand zu beenden, erfanden die Menschen die negativen Zahlen, um sie mitsamt der Null zur Menge der ganzen Zahlen zusammenzufassen, oder um es im Computerlatein auszudrücken: Die Integerzahl war geboren.
Aber gleichzeitig hatte der Mensch damit auch den Bereich der Anschauung verlassen. Die negativen Zahlen stellen abstrakte Gebilde dar, mit denen sich zwar gut rechnen läßt, die aber unser Vorstellungsvermögen bereits auf eine harte Probe stellen. So gab es zum Beispiel während meiner Studienzeit einen Mathematikdozenten, der wegen seiner miserablen Vorlesungen sehr unbeliebt war. Im Laufe des Semesters schmolz sein Publikum zusehends zusammen, bis eines Tages nur noch kümmrliche drei Studenten anwesend waren - und um es kurz zu machen: Die Vorlesung war wieder dermaßen unverständlich, daß insgesamt fünf von ihnen fluchtartig den Raum verließen. 'So', sagte der Prof mit finsterer Miene, 'wenn jetzt noch zwei reinkommen, dann ist keiner mehr da!'
Negative Zahlen sind also irgendwie doof, wie es einer meiner Nachhilfeschüler kurz und bündig zum Ausdruck brachte, aber sie sind auch praktisch, und haben sich deshalb bis heute halten können. Das gleiche gilt sicherlich auch für die rationalen Zahlen, die Menge der Brüche, mit deren Hilfe man problemlos fünf Kühe auf sieben Bauernhöfe verteilen kann - theoretisch zumindest -, aber leider sind damit noch längst nicht alle Probleme beseitigt. Man kann nämlich sehr einfach und schlüssig nachweisen, daß sich die algebraische Gleichung
x2 = 2
nicht durch einen Bruch lösen läßt.
Angenommen, es wäre so, so müßte sich x in der Form p/q darstellen lassen, wobei wir jetzt voraussetzen wollen, daß dieser Bruch bereits so weit wie möglich gekürzt wurde. p und q sind damit teilerfremd, und daran ändert sich auch nichts, wenn wir den Bruch quadrieren. Andererseits erhalten wir nach dem Einsetzen die Aussage
p2 / q2 = 2
Das Ergebnis kann aber nur 2 lauten, wenn sich der Bruch kürzen läßt, was im Widerspruch zu unserer Annahme steht, sie muß deshalb falsch sein. Also blieb den Mathematikern nichts anderes übrig, als für diese und ähnliche Fälle neue Zahlen zu erfinden, die irrationalen Zahlen. Was bedeutet aber eigentlich irrational? Nehmen wir also ein Fremdwörterlexikon zur Hand, und dort finden wir wahrhaftig 'mit dem Verstande nicht erfaßbar, gefühlsbetont, triebhaft'.
Sie merken schon - jetzt wird's gefährlich! Zwar habe ich persönlich an der Wurzel aus 2 noch keine triebhaften Züge entdeckt, doch den Mathematikern müssen diese Zahlen irgendwie unheimlich gewesen sein, denn sie wurden flugs mit den rationalen Zahlen zur Menge der reellen Zahlen vereint , die Sie auf dem CPC als REAL-Typ wiederfinden. Reell heißt soviel wie 'realisierbar, einwandfrei, anständig', Sitte und Ordnung wären also wieder hergestellt, und man könnte sich jetzt in Ruhe anderen Dingen zuwenden, wenn es nicht noch ein kleines Problem gäbe:
x2 = -1
Das ist wirklich eine harte Nuß: Welche Zahl ergibt mit sich selbst multipliziert -1? Mit den reellen Zahlen kommt man keinen Schritt weiter, und auch unser schlauer CPC ist hier überfordert:
PRINT SQR(-1)
entlockt ihm nur ein ratloses Improper Argument.
Doch an dieser nahezu unüberwindlichen Schwelle wagten die Mathematiker einen mutigen Schritt. 'Gut', sagten sie sich, 'wir kennen die Lösung nicht, aber wir wollen einfach mal annehmen, daß eine existiert', und nannten diese geheimnisvolle Zahl i, für die definitionsgemäß gilt
i2 = - 1
Der Buchstabe i steht für imaginär (scheinbar, unwirklich), ein treffender Name für eine absolut abstrakte Zahl, die keine Entsprechung mehr in der Wirklichkeit hat. Doch wie Versuche zeigen, kann man mit der imaginären Zahl alle gewohnten Rechenoperationen durchführen, ohne daß es zu Widersprüchen kommt. Die Erweiterung des Zahlenbegriffs ist damit zumindest formal in Ordnung. Insbesondere ist es möglich, die Zahl i durch Addition oder Multiplikation mit reellen Zahlen zu verknüpfen, wodurch Gebilde wie etwa 3+2*i entstehen, oder in allgemeiner Form
c = x + y * i
Solche Zahlen c, die aus einer reellen Zahl und einem Vielfachen der imaginären Grundeinheit zusammengesetzt sind, nennt man komplexe Zahlen. Dem berühmten Mathematiker Gauß ist der Nachweis zu verdanken, daß damit unser Zahlensystem entgültig abgeschlossen ist; jede algebraische Gleichung hat also zumindest eine komplexe Lösung.
Es fragt sich nur, warum man sich überhaupt mit solchen Hirngespinsten beschäftigen soll, die auf den ersten Blick nicht den geringsten praktischen Wert haben. Doch ähnlich wie die negativen Zahlen stellen die komplexen Zahlen trotz ihrer Unanschaulichkeit für manche physikalischen oder mathematischen Problemstellungen ein sehr effektives Werkzeug dar. So lassen sich zum Beispiel einige Differentialgleichungen wesentlich einfacher lösen, wenn man von vornherein bestimmte Variablen als komplexe Zahlen betrachtet.
Nicht umsonst stellen höhere Programmiersprachen für wissenschaftliche Anwendungen (z.B. FORTRAN) neben INTEGER und REAL auch den Variablentyp COMPLEX zur Verfügung. Obwohl das Locomotive-Basic keine Anweisung wie DEFCOMPLEX kennt, kann man jedoch auch mit dem CPC in die Gefilde der höheren Mathematik vordringen. Jede komplexe Zahl c=x+y*i läßt sich nämlich durch ein ganz normales Zahlenpaar (x,y) darstellen, wobei die eine den Realteil und die andere den Imaginärteil repräsentiert. Indem wir den Rechner die Komponenten separat bearbeiten lassen, ersparen wir ihm die ominöse Wurzel aus -1, die ja sofort einen Error auslösen würde.
Solch ein Zahlenpaar läßt sich natürlich hervorragend in einem Koordinatensystem darstellen, wobei die x-Achse der reellen Zahlengeraden und die y-Achse der imaginaren Geraden entspricht. Zeichnet man vom Ursprung des Koordinatensystems einen Pfeil bis zu dem Punkt, der die komplexe Zahl repräsentiert, so kann man sich noch veranschaulichen, was man unter dem Absolutbetrag dieser Zahl versteht: Er ist identisch mit der Länge des Pfeils, die mit dem Satz des Pythagoras berechnet wird:
L2 = x2 + y2
Auf diese Weise ist es sogar möglich, komplexen Zahlen eine Größe zuzuordnen, die für die Apfelmännchen-Grafik noch eine wichtige Rolle spielen wird.
Ordnung ist das halbe Leben, so sagt ein Sprichwort - und Unordnung die andere Hälfte, ergänzt der erfahrene Programmierer, der nach intensiver Suche die Systemdiskette zwischen ein paar alten Listings im Papierkorb wiederfindet. Doch Schreck beiseite: Heutzutage macht sich in den Naturwissenschaften mehr und mehr die Überzeugung breit, daß hochkomplizierte Strukturen wie lebende Organismen nur durch das Zusammenspiel von Ordnung und Chaos, von Gesetz und Zufall entstehen konnten. Und diese Theorie wird insbesondere durch die Ergebnisse einiger Computersimulationen gestützt!
Die exakten Naturgesetze geben der Welt einen festen Rahmen. Sind alle Anfangsbedingungen eines Systems bekannt, so kann man mit ihrer Hilfe zumindest theoretisch in allen Einzelheiten berechnen, was passieren wird. Doch die moderne Physik hat nachgewiesen, daß im Bereich der Elementarteilchen. Abläufe stattfinden, die unbestimmt sind, und über die höchstens statistische Aussagen gemacht werden können. Unsere Welt besitzt also einen eingebauten Zufallsgenerator, der zuverlässig verhindert, daß sie in gleichbleibenden Mustern stagniert.
Jeder Spiele-Programnierer weiß die RND-Funktionn seines Computers zu schätzen, den vorprogrammierten Unbestimmtheitsfaktor, der für Abwechslung und Spannung sorgt. Bei Bedarf produziert er eine Folge von Zahlen, denen beim besten willen kein System mehr anzusehen ist. Und trotzdem handelt es sich nicht um echten Zufall, sondern nur um eine sehr gute Simulation! Natürlich kann ein Computer sich nicht intuitiv Zahlen ausdenken, sondern muß sie auf irgendeine Weise berechnen.
Eine Folge von Pseudo-Zufallszahlen wird im allgemeinen iterativ erzeugt, d.h. jede Zahl entsteht aus der vorherigen durch ein bestimmtes Bildungsgesetz, das allerdings von Betrachter kaum nachzuvollziehen ist, es sei denn, er schaut sich im ROM-Listing um. Eine einfache Rechenoperation wie das Quadrieren der Zahl reicht hier natürlich nicht, das Bildungsgesetz wäre noch zu offensichtlich. Wesentlich mehr künstliches Chaos entsteht schon, wenn man zusätzlich noch die erste Zahl der Folge als konstanten Wert subtrahiert, wie das folgende Kurzprogramm zeigt:
10 xstart=l.5: x=xstart 20 x=x*x-xstart: PRINT x 30 GOTO 20
Obwohl die recht strengen Kriterien für professionelle Zufallsgeneratoren durch dieses einfache System noch nicht erfüllt sind, ist das Ergebnis schon recht beachtlich, und es wird noch interessanter, wem wir die gleiche Iterationsvorschrift auf konplexe Zahlen anwenden. Um das Gesetz noch einmal exakt zu formulieren: Wenn die komplexe Zahl C der Startwert ist,
C1 = C
dann berechnen wir alle weiteren Zahlen nach der Vorschrift
Cn + 1 = Cn2 - C
Trotz dieser einfachen Darstellung ergibt sich in der Praxis einige Rechnerei. Das Quadrat einer komplexen Zahl muß mit Hilfe der binomischen Formel ermittelt werden:
C2 = (x + yi)2 = x2 + 2xyi + y2i2
Da i * i = -1 ergibt, können wir noch vereinfachen,
c2 = x2 + 2xyi - y2
und dann Real- und Imaginärteil trennen,
Re(c2) = x2 - y2; Im(c2) = 2xy
womit deutlich wird, daß diese Operation insgesamt eine Subtraktion und vier Multiplikationen erfordert. Das Subtrahieren zweier komplexer Zahlen ist glücklicherweise etwas weniger aufwendig; hier werden einfach die Real- und Imaginärkomponenten der beiden zahlen separat voneinander abgezogen.
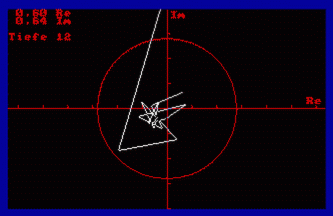
Um zu verstehen, wie diese Rechenoperation das Apfelmännchen und Konsorten erzeugen, sollten Sie sich zunächst das Programm Komplexe Folgen (KOMFOL.BAS) vornehmen. Nach dem Programmstart erscheint auf dem Bildschirm ein Koordinatenkreuz, das durch die reelle und imaginäre Achse der Zahlenebene gebildet wird. Zusätzlich ist ein Kreis und ein heller Punkt zu sehen, der mit den Cursortasten gesteuert wird und den Startwert repräsentiert. Oben links werden Real- und Imaginärteil des augenblicklichen Standortes angezeigt.
Wenn Sie nun mehrmals die <SPACE>-Taste drücken, berechnet das Programm nach der oben angegebenen Methode die jeweils nächste Zahl der Folge und zieht eine Linie zur neuen Position. Je nach Startwert ergibt sich ein wilder Zickzack-Kurs, der allerdings beendet wird, wenn das Abbruchkriterium
x2 + y2 = 8
erfüllt ist, also der Absolutbetrag einer Zahl der komplexen Folge außerhalb des Kreises mit dem Radius Wurzel 8 liegt. Mit DEL können sie das Programm neu starten und einen anderen Anfangswert probieren.

Die Ergebnisse dieser Experimente können sehr verschieden ausfallen. Einige Folgen verlassen schon nach wenigen Iterationen den Kreis, andere erst nach vielem Hin und Her (probieren Sie 0.24 / -0.64!), und manche, deren Anfangswert nahe genug bei 0 liegt, rennen sich fest und erreichen nie das Abbruchkriterium.
Bemerkenwert ist weiterhin, daß sich die Grundmuster in verkleinerter Form an verschiedenen Stellen der Grafik wiederholen. Der große Zusammenhang spiegelt sich im Kleinen wieder - ein wichtiger Grundgedanke der Esoterik und anderer, ganzheitlich orientierter Philosophien, der in diesen Bildern auf verblüffende Weise seinen Ausdruck findet.
Wie wird die komplexe Grafik nun auf dem CPC realisiert? Gehen wir von den technischen Voraussetzungen aus: Der Grafikbildschinn stellt ebenfalls ein Koordinatensystem dar, das in MODE 1 insgesamt 320 * 200 Bildpunkte enthält.
Wenn wir einen Bereich der komplexen Zahlenebene auswählen und auf den Bildschirm projizieren, entspricht jeder Punkt einer Zahl. Sie stellt den Startwert einer komplexen Folge dar, die berechnet wird, bis das Abbruchkriterium
x2 + y2 >= 8
erreicht ist. Für ein komplettes Bild müssen also 64000 Folgen erzeugt werden, für jede Folge abhängig von der Iterationstiefe einige -zig komplexe Zahlen, und das auch noch in der zeitaufwendigen Fließkomma-Arithmetik. Es ist also leicht einzusehen, daß der Zeitaufwand für ein Bild mehrere Stunden betragen kam. Wie Experimente mit dem Programm KOMFOL.BAS zeigen, gibt es allerdinas auch Folgen, die nie das Abbruchkriterium erreichen. Deshalb wird von vornherein eine maximale Tiefe als feste Grenze festgelegt, damit sich das Programm nicht in einer Endlosschleife verfängt.
Alles in allem zeigen die komplexen Folgen also ein recht chaotisches Verhalten, und genau das wollten wir ja auch erreichen. Doch jetzt der Clou: Eines Tages kam der Mathematiker Benoit Mandelbrot im IEM Research-Center New York auf die geniale Idee, die Punkte der komplexen Zahlenebene einzufärben, und zwar in Abhängigkeit von der Iterationstiefe bis zum Abbruch - und er staunte nicht schlecht, als er das Ergebnis sah: Das erste Apfelmännchen war geboren! Die feinen Strukturen am inneren Rand der Figur hielt er übrigens zunächst für Unschärfen, erzeugt durch Rundungsfehler. Erst die Berechnung vergrößerter Auschnitte förderte die erstaunliche Tatsache zu Tage, daß diese Grafik eine unendliche Anzahl kunstvoller Unterstrukturen enthält.
Nach Ermittlung der Anzahl der Iterationsschritte bis zum Abbruch stehen in MODE 1 insgesamt 4 Farben zur Verfügung (PEN 0 bis PEN 3), um die Punkte in Abhängigkeit von der erzielten Rechentiefe mit dem PLOT-Befehl einzufärben. Für die maximale Tiefe kann z.B. PEN 0 verwendet werden; ansonsten sorgt die Formel Farbe = Tiefe MOD 4 dafür, daß sich die Farben zyklisch wiederholen.
Die Berechnungsroutine für das Programm Komplexe Grafik (KOMGRA.BAS) wurde in Maschinensprache geschrieben, um eine hohe Geschwindigkeit zu erreichen. Da man den Algorithmus in dieser Form kaum wiedererkennen kann, finden Sie hier noch ein Basic-Listing, das im wesentlichen dem Maschinenprogramm entspricht. Für den praktischen Einsatz wäre es allerdings viel zu langsam.
10 MODE 1 20 xl = -0.7: xr = 2.1:REM linker und rechter Rand reell 30 yu = -1: yo = 1: REM unterer und oberer Rand imaginär 40 MaxTiefe = 30: REM maximale Iterationstiefe 50 dx = (xr - xl)/319: REM X-Schrittweite 60 dy = (yo - yu)/199: REM Y-Schrittweite 70 y = yu 80 FOR Zeile = 0 TO 199 90 x = xl 100 FOR Spalte = 0 TO 319 110 Tiefe = 0: re2 = x*x: im2 = y*y 120 WHILE (Tiefe < MaxTiefe) AND (re2 + im2 < 8) 130 re = re2 - im2 - x: im = 2*re*im - y 140 re2 = re*re: im2 = im*im: Tiefe = Tiefe + 1 150 WEND 160 IF Tiefe = MaxTiefe THEN f = 0 ELSE f = Tiefe MDD 4 170 PLOT 2*Spalte,2*Zeile,f 180 x = x + dx 190 NEXT Spalte 200 y = y + dy 210 NEXT Zeile
Und jetzt zur Bedienung des Programms Komplexe Grafik: Nach dem Programmstart erscheint auf dem Bildschirm ein kleines Menuefenster. Es handelt sich um ein Pull Down-Menue, das man jederzeit mit Hilfe der <ENTER>-Taste aufrufen oder verschwinden lassen kann, ohne daß die Grafik zerstört wird. Die einzelnen Menuepunkte werden mit Hilfe eines Pointers angewählt, der mit den Cursortasten <oben> und <unten> bewegt wird. Die <COPY>-Taste aktiviert die Funktion, auf die der Pointer zeigt.
Um das Apfelmännchen als Grundlage für weitere Bilder zu erzeugen, wählen Sie am besten direkt den Punkt Zeichnen an. Danach will das Programm noch die maximale Iterationstiefe wissen; geben Sie hier den Wert 30 ein und drücken <ENTER>. Der CPC wird sich daraufhin etwa eine Stunde lang mit dem Bild beschäftigen.

Wenn es fertig ist, erscheint wieder das Menuefenster, und Sie können mit der Funktion Speichern die Grafik nach Eingabe eines Dateinamens auf Kassette oder Diskette sichern. An den Namen hängt das Programm selbsttätig die Erweiterung .PIC (Picture) an, um das Binärfile als Bilddatei zu markieren. Auch beim Laden dürfen Sie die Kennzeichnung nicht mit eingegeben, da sie das Programm von sich aus ergänzt! Beim Speichern auf Diskette sollte man sich unbedingt davon überzeugen,.daß der Name korrekt ist und sich wirklich eine Diskette im Laufwerk befindet, da sonst das Bild durch die Fehlermeldung zerstört wird.
Beim Speichern werden übrigens alle wichtigen Bilddaten (Farben, Koordinaten, Tiefe) mit aufgezeichnet. Ein Trick erspart hier zusätzliche Parameterdateien: Die Werte stehen nämlich in einem nicht sichtbaren Bereich des Bildschirmspeichers! Nach dem Laden werden sie dann wieder gelesen und korrekt eingestellt. Dadurch ist es sogar möglich, ein unvollständiges Bild abzuspeichern und bei Gelegenheit weiterzeichnen zu lassen. Der Abbruch erfolgt mit <ENTER>, der CPC reagiert allerdings erst, wenn er mit der aktuellen Rasterzeile fertig ist, was mitunter etwas dauern kann. Eine unvollständige Grafik im Speicher wird vom Programm automatisch erkannt; nach Anwahl von Zeichnen setzt er sein Werk fort, ohne voher dumme Fragen zu stellen.
Der Menuepunkt Farben ermöglicht es, mit Hilfe der Cursortasten <oben> und <unten> die vier Farbstifte (PEN) anzusteuern und dann mit den Tasten <links> bzw. <rechts> die dazugehörige Farbe (INK) zu ändern. Angezeigt wird dabei laufend die Nummer der Farbe - siehe CPC-Anleitungsbuch. Mit ENTER kommen Sie zurück ins Hauptmenue.
Die Funktion Ausschnitt bietet die Möglichkeit, einen bestimmten Bereich der komplexen Zahlenebene herauszugreifen, um ihn entsprechend vergrößert zeichnen zu lassen. Wenn sich bereits ein Bild im Speicher befindet, so wird ein Rechteck auf dem Bildschirm erscheinen, das Sie mit den Cursortasten herumwandern lassen können. Für die Feinabstimmmg sind die Cursortasten plus SHIFT bzw. CTRL zuständig; auf diese Weise wird die obere linke bzw. untere rechte Ecke des Ausschnitts pixelweise verschoben. Die Form und Größe des Rechtecks kann damit beliebig verändert werden. Es empfiehlt sich jedoch, ein Seitenverhältnis zu wählen, das ungefähr dem Bildschirmformat entspricht, damit beim Zeichnen nicht starke Verzerrungen entstehen.
Wer sich für die Koordination des Ausschnitts interessiert, kann die Werte einfach mit COPY abrufen; eine beliebige Taste läßt sie wieder vom Bildschirm verschwinden. mit ENTER wird die Wahl des Ausschnitts abgeschlossen, und das Menue erscheint. Wenn Sie den Punkt Ausschnitt anwählen, ohne daß sich ein Bild Im Speicher befindet, ergibt das Rechteck natürlich keinen Sinn. Das Programm erwartet in diesem Fall von Ihnen, daß Sie den Bereich durch die Eingabe von vier Zahlen bestimmen: linker Rand; rechter Rand; oberer Rand; unterer Rand
<ENTER> ohne eine Eingabe führt auch hier zurück ins Hauptmenue. Der Programmteil Zeichnen erzeugt immer den zuletzt eingestellten Ausschnitt. Wenn Sie nach dem Programmstart keinen Bereich vorgeben, wird, wie bereits erwähnt, automatisch das Apfelmännchen mit folgenden Koordinaten gemalt:
links = -0.7; rechts = 2.1; unten = -1.0; oben = 1.0
Wenn das Programm ein neues Bild zeichnet, so wird das alte Bild einfach überschrieben.Es bleibt also noch auf dem Bildschirm, es sei denn, Sie wählen zunächst den Punkt Löschen. Diese Funktion löscht das Bild, nicht aber einen vorher eingestellten Ausschnitt!
Für das nächste Bild sucht man sich am besten einen Bereich aus, der schon von vornherein eine interessante Struktur erkennen läßt. Von den Vergroßerungen kann man natürlich weitere Ausschnitte zeichnen lassen und auf diese Weise immer weiter in Bilddetails vordringen, soweit die Rechengenauigkeit des CPC reicht.
Insbesondere der innere Rand des Apfelmännchens gibt allerhand her. Wem Sie nach Wahl des Menuepunktes Zeichnen eine größere Rechentiefe vorgeben (maximal 255), kommen weitere Formen zum Vorschein: Je größer die Tiefe, um so mehr Strukturen kann das Programm erfassen. Allerdings steigt damit auch die Rechenzeit für ein komplettes Bild enorm an und kann sich bis auf mehrere Stunden ausdehnen. Etwas Geduld braucht man also schon für dieses Abenteuer im Land der komplexen Zahlen!
Interessante Koordinaten zum Ausprobieren:
| links | rechts | oben | unten | Tiefe |
|---|---|---|---|---|
| 1.778 | 1.793 | 0.0069 | -0.0069 | 30 |
| 0.038 | 0.103 | 0.834 | 0.845 | 60 |
| 0.090649 | 0.09416 | 0.84146 | 0.84378 | 60 |
| 0.09282 | 0.094321 | -0.84301 | -0.84329 | 90 |
| 0.7445 | 0.7459 | -0.1121 | -0.1132 | 200 |
Literaturhinweis: